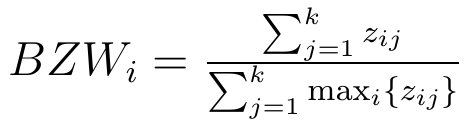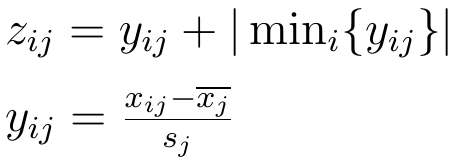Względny poziom rozwoju bez wzorca

Omówimy dziś tzw. wskaźnik względnego poziomu rozwoju bez wzorca. Jest to narzędzie z obszaru analizy wielokryterialnej, które umożliwia porównywanie obiektów (np. przedsiębiorstw) opisanych uprzednio przy pomocy pewnych kryteriów (np. wskaźników ekonomicznych).

Na naszych łamach omawialiśmy już wiele metod wielokryterialnych:

- SAW (metoda średniej ważonej)
- MOORA (Multi-Objective Optimization on the basis of Ratio Analysis)
- COPRAS (COmplex PRoportional ASsesment)
- ARAS (Additive Ratio Assesment)
- WASPAS (Weighted Aggregated Sum Product Assessment)
- SPR-2T
- VIKOR (VIseKriterijumska Optimizacija I Kompromisno Resenje)
- algorytm Bordy
- ELECTRE (ELiminiation Et Choix Traduisant la REalite)
- TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution)
- TMAI (Taksonomiczna Miara Atrakcyjności Inwestowania).

Niektóre z tych algorytmów (np. ARAS, TMAI, TOPSIS czy VIKOR) bazują na koncepcji tzw. wzorca idealnego (ew. dwóch wzorców: idealnego i antyidealnego). W uproszczeniu chodzi o to, że każdy obiekt (spółkę) porównujemy z pewnym obiektem modelowym, który nie istnieje, ale który zbudowano w oparciu o najlepsze wyniki rzeczywistych podmiotów. Innymi słowy: najpierw z faktycznej puli wybieramy najlepsze odczyty każdego kryterium (może być np. tak, że najlepszą płynność bieżącą ma spółka A, spółka B wygrywa w kategoriach rentowności netto i operacyjnej itd.). Później zestaw tych najlepszych wyników traktujemy jako hipotetyczną spółkę wzorcową. Następnie - przy pomocy mniej lub bardziej skomplikowanych formuł matematycznych - mierzymy "odległość" każdej firmy od wzorca. Im bliżej, tym lepiej to o podmiocie świadczy. W teorii może być nawet tak, że któraś z firm celuje we wszystkich kryteriach: wtedy jest ona tożsama z wzorcem i taka odległość wyniesie 0 (albo 1, jeżeli wcześniej przetworzyliśmy formułę tak, by najlepsze były wysokie wyniki).

Wspominamy o tym wszystkim jedynie po to, aby uwypuklić fakt, że dziś zajmiemy się metodą, która nie korzysta z takiego wzorca. Co prawda wskaźnik względnego poziomu rozwoju bez wzorca (BZW) daje nam znormalizowane wartości w zakresie [0, 1], ale obywa się bez jakiegokolwiek idealnego modelu. Po prostu: im wyższy rezultat, tym lepiej świadczy to o badanym obiekcie.

Wzór wygląda następująco:

Oczywiście wypada wyjaśnić zastosowane oznaczenia. Są one takie:

Naturalnie to wciąż wygląda enigmatycznie. A zatem zacznijmy od tego, że mamy n obiektów (np. spółek) indeksowanych literką i, a zarazem k kryteriów (indeksowanych przy pomocy j). Przez x_ij rozumiemy wartość j-tego kryterium dla i-tej spółki. Jeżeli więc np. kryterium nr 2 to rentowność netto, a spółka nr 3 to Impexmetal, wówczas x₃₂ będzie oznaczać rentowność netto Impexmetalu (np. w roku 2018). Przyjmujemy przy tym, że każde kryterium ma charakter stymulanty: to znaczy, im wyższy odczyt, tym lepiej.

Każda wyjściowa wartość x_ij jest normalizowana w ten sposób, że odejmuje się od niej średnią dla j-tego kryterium (z wszystkich badanych obiektów) i dzieli przez odchylenie standardowe dla tegoż kryterium. Tak powstają wartości y_ij. Po takiej standaryzacji po standaryzacji zmienna będzie mieć wariancję 1 i średnią 0. Później rozważamy minimalną wartość y_ij spośród wszystkich spółek, bierzemy wartość bezwzględną tej wielkości, dodajemy otrzymaną liczbę do y_ij - i dostajemy z_ij.

Wreszcie przechodzimy do obliczania W_i, czyli wartości wskaźnika dla i-tej spółki. To ułamek. W liczniku sumujemy (przetransformowane już do postaci z_ij) wartości kryteriów dla tejże spółki, natomiast mianownik jest dla każdego przypadku taki sam: to suma maksymalnych z_ij po wszystkich kryteriach.

Im wyższy wynik, tym lepsza spółka: tak się interpretuje uzyskany wskaźnik. Gorsze podmioty mają niższe wyniki. Nigdy dość przypominania, że ten ranking nie jest i nie może być całkowicie obiektywny. To znaczy: wyniki są dobre lub złe w świetle danej metody. Tylko tyle i aż tyle. Na pocieszenie można jednak powiedzieć, że metody MCDM (multi-criteria decision making) zwykle buduje się tak, by pasowały do naszych intuicji (np. firma, która ma ciężką stratę, kiepską płynność i potężne zadłużenie powinna uzyskać słaby rezultat). Co więcej, w praktyce powoduje to, że rankingi liczone według różnych algorytmów rzadko kiedy są od siebie skrajnie różne.

*

A teraz przykład praktyczny. Rozważmy sześć spółek przemysłowych z głównego parkietu GPW pod kątem ich skonsolidowanych wyników za rok 2018. Oto Alchemia, Elektrotim, Impexmetal, Konsorcjum Stali, Rafamet i Stalprofil (alfabetycznie).

Badamy osiem wskaźników:

1) rentowność operacyjna: zysk operacyjny / przychody

2) rentowność netto: zysk netto / przychody

3) płynność bieżąca: aktywa obrotowe / zobowiązania krótkoterminowe

4) zadłużenie ogólne: zobowiązania / suma bilansowa

5) wypłacalność natychmiastowa: środki pieniężne / zobowiązania krótkoterminowe

6) ROE (zwrot z kapitału): zysk netto / stan kapitału własnego pod koniec minionego roku obrotowego

7) ROA (zwrot z aktywów): zysk netto / stan aktywów pod koniec minionego roku obrotowego

8) złota reguła bilansowa: kapitał własny / aktywa trwałe (reguła jest wypełniona, gdy wskaźnik ma wartość wyższą niż 1 pkt)

Wartości wskaźników podaliśmy w formie ułamków dziesiętnych z dokładnością do 4 miejsc po przecinku. Na przykład rentowność operacyjna Stalprofilu to 2,84 proc., a zadłużenie ogólne Impexmetalu to 34 proc. Zadłużenie jest w każdym przypadku ujemne. Dlaczego? Otóż wyjściowo to kryterium traktujemy jako destymulantę. Im niższe zadłużenie, tym lepiej, im wyższe, tym gorzej. Dokonaliśmy jednak transformacji tej zmiennej w stymulantę, stosując najprostszą formułę, tj. zmianę znaku. W ten sposób np. 34-procentowe zadłużenie (0,34 pkt) zmienia się w -0,34 pkt.

W drugiej tabeli mamy wyliczone pośrednie wartości, tj. y_ij z ogólnego wzoru. Korzystamy przy tym ze średniej i odchylenia standardowego (dla kolejnych kryteriów po wszystkich spółkach).

W trzeciej tabeli wyliczamy z_ij, dodając do każdego y_ij moduł z minimalnej wartości y_ij dla j-tego kryterium. Zauważmy, że w każdej kolumnie jedna wartość (właśnie ta minimalna) siłą rzeczy stanie się zerowa. Teoretycznie takich wartości mogłoby być więcej, choć de facto taka zgodność spółek jest mało prawdopodobna.

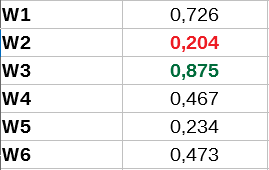
Uzyskane wartości podstawiamy do końcowego wzoru na W_i, przez co otrzymujemy następującą tabelkę:

Wychodzi na to, że "średnio" (w sensie metody BZW) najlepszy podmiot to Impexmetal (0,757 pkt), zaś najgorszy to Elektrotim (0,204 pkt). Ostateczny ranking jest taki (od najsłabszej do najmocniejszej firmy): --- Elektrotim, Rafamet, Konsorcjum Stali, Stalprofil, Alchemia, Impexmetal. Dodajmy na koniec, że wszystkie kryteria były traktowane jako jednakowo ważne: nie było ich ważenia.


Adam Witczak


BIBLIOGRAFIA:

M. Balcerowicz-Szkutnik, E. Sojka, "Metody ilościowe w finansach i rachunkowości", Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2011.

A. Mastalerz-Kodzis, E. Pośpiech, "Zastosowanie wybranych elementów analizy fundamentalnej do wyznaczania portfeli optymalnych", w: Studia Ekonomiczne, Zeszyty Naukowe Wydziałowe nr 146, "Innowacje w finansach i ubezpieczeniach - metody matematyczne i informatyczne", Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2013.

M. Wójciak, "Konkurencyjność działów produkcyjnych polskiej gospodarki", Wydawnictwo Akademii Ekonomicznej w Katowicach 2002.