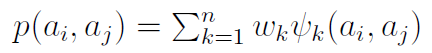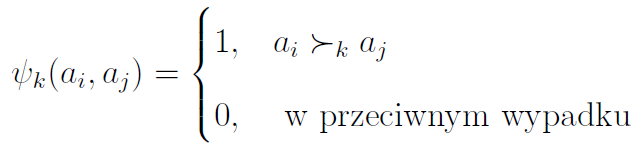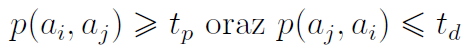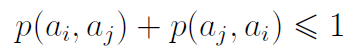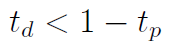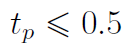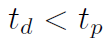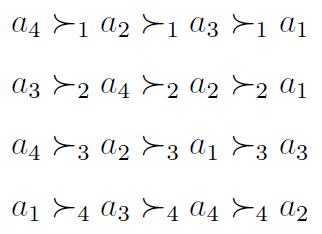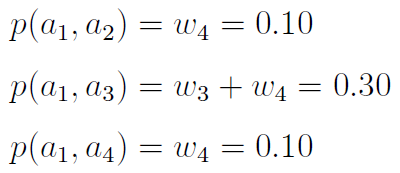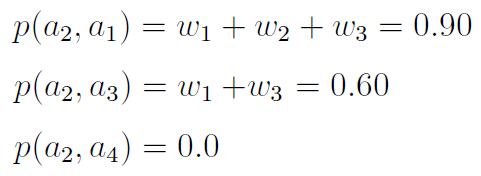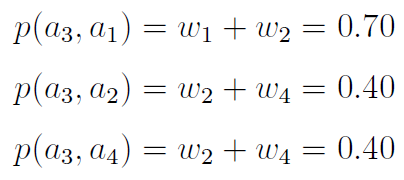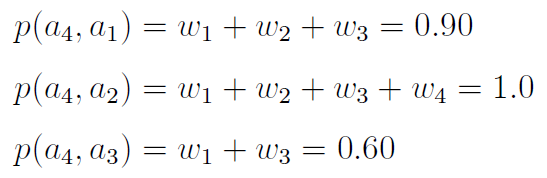Metoda SPR-2T w analizie wielokryterialnej

SPR-2T to metoda analizy wielokryterialnej podobna w swych założeniach i konstrukcji do znanej techniki ELECTRE. Rozważamy następujące zagadnienie: mamy m scenariuszy (wariantów, np. nieruchomości czy społek giełdowych), które oceniane są według n kryteriów. Niektóre scenariusze są lepsze od innych pod pewnymi względami, a pod pozostałymi - gorsze. Decydentowi trudno "na oko" uszeregować te warianty od najlepszych do najgorszych w jakimś "ogólnym" sensie.

Wtedy z pomocą przychodzą techniki MCDM (multi-criteria decision making). Metoda SPR-2T została opracowana przez J. Michnika i M. Lo, którzy opisali ją w pracy "The assessment of the information quality with the aid of multiple criteria analysis", opublikowanej w roku 2009. My prezentujemy ten algorytm według opisu zawartego w książce J. Michnika "Wielokryterialne metody wspomagania decyzji w procesie innowacji".

A zatem, jak już powiedzieliśmy, mamy skończoną liczbę wariantów (ozn. a_i) oraz skończoną liczbę n kryteriów. Zakładamy, że dla każdego kryterium zachodzi pomiędzy każdymi dwoma scenariuszami relacja silnej preferencji.

Na przykład: mamy trzy firmy A, B i C - oraz dwa kryteria, mianowicie rentowność netto i wskaźnik płynności bieżącej.  Rentowność spółki A jest ostro większa niż rentowność spółki C (zapisujemy to A >₁ C), zaś płynność bieżąca spółki B jest ostro większa niż płynność spółki A (B >₂A). Oczywiście relacja ta z natury rzeczy nie może być symetryczna: jeżeli A >_k C, to z pewnością nie jest tak, że C >_k A.

Dla każdej pary uporządkowanej wariantów obliczamy tzw. wskaźnik preferencji p:

Przyjrzyjmy się tej formule. Przez w_k rozumiemy wagę (ważność), jaka została przypisana k-temu kryterium. Wagi powinny być znormalizowane w taki sposób, by sumowały się do 1.

Co się tyczy ψ_k, to jest to funkcja definiowana następująco:

A zatem funkcja ta przyjmuje wartość 1 dla pary (a_i, a_j) wtedy i tylko wtedy, gdy według k-tego kryterium opcja a_i jest wyraźnie lepsza niż a_j.

Następnie wprowadza się tzw. próg preferencji, oznaczony jako t_p. Drugi próg to próg sprzeciwu, ozn. t_d. Uznamy, że wariant a_i przewyższa wariant a_j wtedy i tylko wtedy, gdy zajdzie zależność:

Tak więc: żądamy, by wskaźnik preferencji dla a_i był co najmniej taki jak próg preferencji - i żeby był co najwyżej taki jak próg sprzeciwu.

Zauważmy, że zawsze:

W związku z tym naturalne jest żądanie, by zachodziła poniższa nierówność:

A w dodatku, jeżeli akurat:

...to wówczas:

Ostatecznie chodzi o to, by suma wag kryteriów, według których a_i jest lepsze niż a_j była dostatecznie duża, a suma tych, w których a_j jednak przeważa, była wystarczająco mała. Tak więc oczyszczamy pierwotną bazę danych, by móc powiedzieć, że np. wariant A jest "średnio" czy "ogólnie" lepszy od B, a B "ogólnie" lepszy niż C.

To, jak dobiera się wagi i progi, to odrębna sprawa, której nie będziemy tu poruszać. Gdy brak lepszego pomysłu, można oczywiście uznać, że kryteria są równoważne (każda waga to wtedy 1/n). Można też eksperymentować z różnymi wartościami wag oraz t_p i t_d - a następnie porównywać je choćby z narzucającą się intuicją.

*

Przeanalizujmy pewien przykład - najzupełniej fikcyjny. Załóżmy, że mamy 4 scenariusze i 4 kryteria. Układ relacji preferencji jest taki:

Widzimy np., że wariant nr 4 jest lepszy od wszystkich pozostałych według kryteriów 1 i 3, a wariant nr 1 jest gorszy od wszystkich pozostałych według kryteriów 1 i 2. Równocześnie wariant nr 1 przeważa nad nr 3 w świetle kryterium 3.

Arbitralnie przyjmijmy następujące ważności: w₁ = 0.40, w₂ = 0.30, w₃ = 0.20 oraz w₄ = 0.10. Jak widać, pierwsze kryterium jest dla nas kluczowe, ostatnie tylko niuansowe. A zatem wariant nr 1 jest najlepszy tylko pod tym mało istotnym względem.

Przyjmijmy zarazem następujące progi: t_p = 0.51 oraz t_d = 0.35.

Obliczmy wskaźniki preferencji według zaprezentowanego wcześniej wzoru:

W powyższym zestawieniu mamy 0 na każdej takiej pozycji o indeksie i-j, że i-ty scenariusz nie przeważa nad j-tym - oraz 1 na każdej takiej, że przeważa.

Dla przykładu: na pozycji 3_1 (trzeci wiersz, pierwsza kolumna) mamy 1, ponieważ p(a₃, a₁) = 0,70 > 0,51 oraz p(a₁, a₃) = 0.30 < 0.35.

Adam Witczak

BIBLIOGRAFIA:

A. Kobryń, "Wielokryterialne wspomaganie decyzji w gospodarowaniu przestrzenią", Difin 2014.

J. Michnik, "Wielokryterialne metody wspomagania decyzji", Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2013.

Michnik J., Lo M. (2009), The assessment of the information quality with the aid of multiple criteria analysis, European Journal of Operational research, Vol. 195(3).