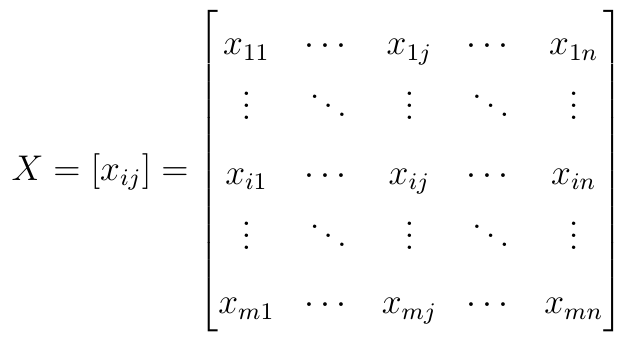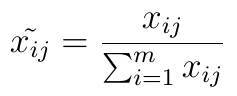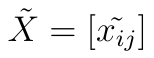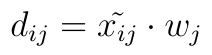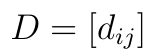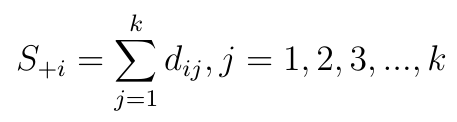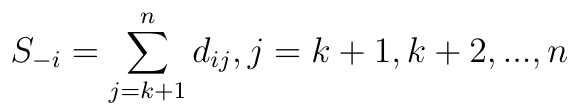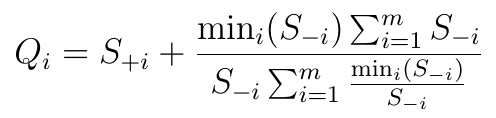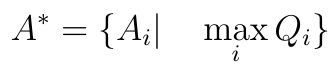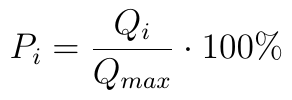Wybór algorytmem COPRAS

COPRAS to kolejna metoda wielokryterialna, która wywodzi się z Litwy, z kręgu tamtejszych informatyków i matematyków. Kolejna, bo na naszych łamach prezentowaliśmy już algorytmy WASPAS i ARAS.

Akronim COPRAS rozwija się następująco: COmplex PRoportional ASsesment. Metoda po raz pierwszy zaprezentowana została w roku 1994 w pracy E. K. Zavadskasa, A. Kaklauskasa i V. Sarki "The new method of multi-criteria complex proportional assessment of project".

Na podstawie prac podanych w bibliografii zaprezentujemy podstawowe kroki algorytmu COPRAS. Zaczynamy od bazowej macierzy decyzyjnej:

Macierz ta ma m wierszy oraz n kolumn. Oznacza to m scenariuszy, które badamy według n kryteriów. Na przykład m = 5, n = 3 i badamy pięć społek giełdowych w odniesieniu do ich rocznej rentowności netto, płynności bieżącej i sumy aktywów.

Wartości w macierzy trzeba znormalizować. To dlatego, że kryteria mogą się (wyjściowo) wyrażać liczbami rożnych rzędów. W COPRAS stosuje się następujący wzór normalizacyjny:

Innymi słowy, każdą wartość dzielimy przez sumę wszystkich wartości w kolumnie. To znaczy, że w mianowniku ułamka sumujemy po scenariuszach, a za to przy ustalonym kryterium. Wynik trafia (co do wartości bezwzględnej) w zakres [0, 1].

Zauważmy, że - w przeciwieństwie do ARAS, WASPAS i wielu innych metod - normalizacja przebiega tak samo dla stymulant i destymulant. Przypomnijmy, że stymulanty to kryteria, które chcemy maksymalizować, a destymulanty to te, które chcemy minimalizować. Na przykład rentowność zwykle jest stymulantą, a zadłużenie - destymulantą.

Teraz możemy dla formalności rozważyć macierz danych znormalizowanych, w skrócie zapisując ją w ten sposób:

To jednak nie wystarczy. Kryteria zazwyczaj różnią się istotnością. Każde ma swoją własną wagę, a wszystkie te wagi powinny sumować się do 1 (np. 2/5 + 1/2 + 1/10 dla trzech kryteriów). Teraz więc przygotowujemy elementy macierzy znormalizowanej i zarazem zważonej:

Jak widać, każdą znormalizowaną wartość mnożymy przez wagę typową dla odpowiadającego jej kryterium. Macierz, która w ten sposób powstaje, można symbolicznie przedstawić tak:

W kolejnym kroku uwzględnimy różnicę pomiędzy stymulantami a destymulantami. Zakładamy przy tym, że stymulanty to pierwszych k kolumn macierzy, natomiast od k+1 do n mamy destymulanty. Naturalnie macierz zawsze można w ten sposób uporządkować.

Dla stymulant obliczamy wielkość S+i:

W przypadku destymulant liczymy S_-i:

Innymi słowy, dla każdego i-tego scenariusza (np. i-tej spółki): osobno sumujemy zważone i znormalizowane wartości z puli stymulant - i osobno zważone i znormalizowane wartości z destymulant.

Dopiero w tym momencie przechodzimy do clou metody COPRAS. Otóż każdej (i-tej) alternatywie przypisujemy następującą wielkość:

Funkcja ta (waga względna, relative weight) jest dość skomplikowana, a przynajmniej tak można opisać drugi składnik sumy. Nie będziemy tu wnikać w to, dlaczego litewscy badacze wybrali akurat taką formułę.

Jeżeli Qp > Q_r, to znaczy, że p-ty scenariusz jest lepszy niż alternatywa o numerze r. Ostatecznie jest tak, że najlepsze scenariusze to te, które mają najwyższą wartość funkcji wagi względnej. Te najlepsze alternatywy można zebrać w jednym zbiorze:

Dodatkowo dla każdej i-tej alternatywy możemy obliczyć jej stosunek do alternatywy najlepszej (do wartości Q_max, która rzecz jasna jest wspólna dla czołowych, równoprawnych scenariuszy):

Wskaźnik ten, jak widać, możemy przedstawić w ujęciu procentowym. Jeżeli natomiast chodzi o perspektywy i warianty metody COPRAS, to powstało co najmniej kilka dróg jej rozwoju. Istnieje np. algorytm COPRAS-G, oparty o teorię tzw. zbiorów szarych (grey sets). Zbudowano również hybrydową metodę SWARA-COPRAS, w której wagi kryteriów określa się przy pomocy algorytmu SWARA, tj. Step-Wise weight Assessment Ratio Analysis (którego jednak tu nie będziemy prezentować).


Adam Witczak


BIBLIOGRAFIA:

M. Madic, D. Markovic, G. Petrovic, M. Radovanovic, "Application of COPRAS method for supplier selection", The Fifth International Conference Transport and Logistics, 2014.

A. Organ, E. Yalcin, "Performance Evaluation of Research Assistants By COPRAS method", European Scientific Journal, August 2016.

V. Podvezko, "The Comparative Analysis of MCDA Methods SAW and COPRAS", Inzinerine Ekonomika - Engineering Economics, 2011, 22(2), 134 - 146.

J. Stankeviciene, L. Kraujaliene, "COPRAS Approach for Efficiency Assessment of R&D Expenditures Technology Transfer Process", Contemporary Issues in Business, Management and Education 2017

A. Valipour, N. Yahaya, N. Md Noor, J. Antucheviciene, "Hybrid SWARA-COPRAS method for risk assessment in deep foundation excavation project: an Iranian case study", Journal of Civil Engineering and Management, May 2017.

E. K. Zavadskas, Z. Turskis, J. Tamosaitiene, "Risk assessment of construction projects", Journal of Civil Engineering and Management, 16:1, 33-46 (2010).