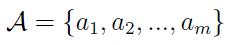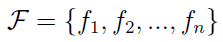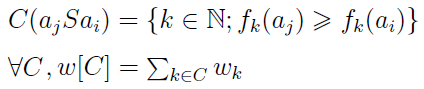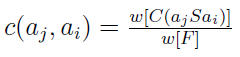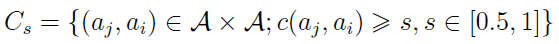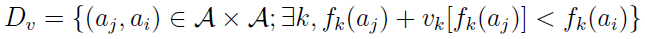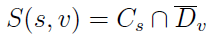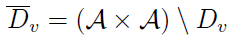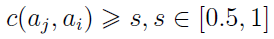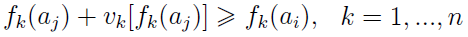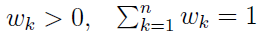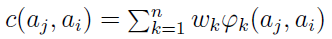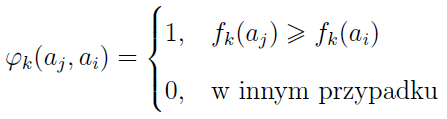Metoda ELECTRE i analiza wielokryterialna

ELECTRE to jedna z metod wielokryterialnego wspomagania decyzji. Takich metod opracowano bardzo dużo, przy czym niemal każda ma przynajmniej kilka odmian.

Najbardziej znane podejścia to PROMETHEE, AHP, ANP, TOPSIS, BIPOLAR, VIKOR czy metoda Bordy. W niektórych przypadkach nazwa niesie ze sobą pewne intrygujące skojarzenia, choć równocześnie pełni rolę skrótu. Tak np. PROMETHEE brzmi cokolwiek prometejsko, ale pod tym zapisem kryje się następujący opis: Preference Ranking Organization METHod for Enrichment of Evaluations. TOPSIS to skrót od Technique for Order of Preference by Similarity to Ideal Solution.

Oczywiście to tylko detale estetyczne, tym niemniej wypada powiedzieć, że ELECTRE to nie tylko "elektryzujące" słówko, ale i skrót od ELiminiation Et Choix Traduisant la REalite. Jak widać, w tym wypadku mamy do czynienia z językiem francuskim. Głównym twórcą tego podejścia jest B. Roy, który zaproponował je w latach 60-tych XX wieku. Później ta metoda była rozwijana także przez innych uczonych, w tym współpracowników i uczniów p. Roya.

*

Tak naprawdę ELECTRE to cała rodzina metod: można wyróżnić ELECTRE I, II, III i IV, a także odmiany IS i TRI. My zajmiemy się podstawowym modelem, czyli ELECTRE I.

Jak wspomnieliśmy, chodzi o analizę wielokryterialną. Ogólny opis problemu jest dość intuicyjny i prosty. Rozważamy zagadnienie, które jest pewnym wyborem. Może to być wybór portfela inwestycyjnego, nieruchomości pod zakup, dostawcy towaru czy strategii marketingowej. Możliwości jest kilka, kilkanaście - lub jeszcze więcej. To są tzw. scenariusze czy też warianty decyzyjne. Każdą z nich oceniamy według ustalonego zestawu kryteriów. Na przykład w przypadku nieruchomości może nas interesować cena za metr kwadratowy, cena całkowita, powierzchnia, kubatura, stan techniczny budynku (o ile potrafimy ocenić go przy pomocy jakiejś sensownej skali), odległość od centrum miasta, zadłużenie obiektu. W przypadku strategii marketingowej może to być jej koszt, liczba pracowników, których trzeba zaangażować, czas realizacji i oczekiwane korzyści (np. zakładany wzrost przychodów ze sprzedaży czy liczby klientów).

Sprawa szybko się komplikuje i wybór "na wyczucie" staje się trudny. Ta nieruchomość jest tańsza, ale raczej zbyt mała; ta druga jest większa, ale dużo droższa, choć nie w przeliczeniu na metr kwadratowy; trzecia wydaje się optymalna, ale jest w nieco gorszym stanie od dwóch poprzednich. I tak dalej.

W tej sytuacji trzeba sobie pomóc przy pomocy jakiegoś algorytmu. Faktycznym jego wykonawcą będzie zapewne komputer, ale trzeba mu wpierw dać przepis.

Przejdźmy do rzeczy. Załóżmy wpierw, że mamy skończony zbiór scenariuszy, tj. wariantów decyzyjnych:

Jest ich m, natomiast kryteriów decyzyjnych mamy n (oczywiście w szczególnym przypadku obie liczby mogą być równe, ale nie ma to większego znaczenia, są one od siebie zupełnie niezależne):

Poszczególne warianty będziemy określać zazwyczaj jako a_i, a_j - zaś poszczególne kryteria jako f_k, f_l. Każde kryterium to w istocie funkcja f_k(a_i), która pobiera scenariusz i zwraca nam wartość dla niego. Na przykład: dla nieruchomości a₄ kryterium drugie (f₂, przyjmijmy, że to cena metra kwadratowego) wynosi f₂(a₄) = 2.900 (zł). Z kolei kryterium trzecie (f₃, załóżmy, że chodzi o metraż) to f₃(a₄) = 120 (metrów kwadratowych). Natomiast dla nieruchomości pierwszej, a₁, możemy mieć np. f₂(a₁) = 2450 zł i f₃(a₁) = 95 m. kw.

Interesuje nas relacja S pomiędzy (dwoma) wariantami - tzn. relacja przewyższania. Jak pisze M. Nowak, odpowiada ona "istnieniu ważnych przesłanek, które uzasadniają preferencję albo przypuszczenie preferencji jednego z dwóch wariantów, lecz bez możliwości rozróżnienia sytuacji silnej i słabej preferencji oraz równoważności". Za parę chwil pogłębimy tę definicję.

Oprócz wariantów i kryteriów mamy jeszcze ważności czy też wagi przypisane poszczególnym kryteriom. Na razie rozważamy model ogólny, w którym są one po prostu liczbami dodatnimi (rzeczywistami, choć oczywiście najprościej pracuje się na naturalnych, np. 3, 7, 1, 4 etc.). Te wagi oznaczamy jako w_k, po jednej dla k-tego kryterium f_k.

*

Przyjmijmy następujące definicje:

W pierwszej linijce określiliśmy zbiór C(a_j S a_i). Wrzucamy do niego te wskaźniki k (numery kryteriów), które spełniają następujący warunek: k-te kryterium dla wariantu j-tego przyjmuje wartość nie niższą (większą lub równą) niż dla wariantu i-tego. Na przykład, biorąc pod uwagę wprowadzone wcześniej ad hoc wartości: f₃(a₄) jest większe niż f₃(a₁), bo 120 > 95, zatem wskaźnik nr 3 (dotyczący kryterium metrażu) trafi do zbioru C(a₄ S a₁). To znaczy: według 3-go kryterium czwarta nieruchomość przewyższa pierwszą, a przynajmniej nie jest od niej słabsza (o ile oczywiście interesuje nas maksymalizacja metrażu).

Taki zbiór C budujemy dla każdej pary wariantów. Są to pary uporządkowane, czyli C(a_j S a_i) może być inny niż C(a_i S a_j). Następnie - linijka druga - każdemu C przypisujemy zbiór w[C], czyli sumę ważności kryteriów, których numery trafiły do C. Swoją drogą, w uproszczeniu moglibyśmy powiedzieć, że to same kryteria trafiają do C, jedynie z powodu matematycznej ścisłości mówimy o ich wskaźnikach (indeksach, numerach).

Teraz wprowadzamy pojęcie współczynnika zgodności:

Jego idea jest taka: dzielimy ważność zbioru C(a_j S a_i) przez łączną ważność wszystkich kryteriów. Może się np. okazać, że w zbiorze C(a₅ S a₃) - grupującym te kryteria, według których a₅ nie jest gorsze niż a₃ - ważność będzie bardzo niska, będą to jakieś niuansowe, trzeciorzędne kwestie.

Zdefiniujmy teraz dwa zbiory (podzbiory produktu kartezjańskiego kolekcji scenariuszy):

Pierwszy z nich to tzw. zbiór zgodności. Trafiają do niego te pary wariantów, dla których współczynnik zgodności jest większy lub równy od pewnej ustalonej wartości progowej s. Zwyczajowo przyjmuje się, że powinna to być co najmniej 1/2. Oczywiście tak czy inaczej s nie może przekroczyć liczby 1.

W definicji drugiego zbioru pojawia się v_k. To tzw. próg weta. Wyobraźmy sobie, że - odwołajmy się znów do wprowadzonych już oznaczeń - próg weta dla kryterium metrażu to 20 (metrów kw.). Załóżmy, że nieruchomość a₁ przewyższa a₄ pod względem prawie każdego kryterium, np. z pięciu powodów, poza powodem nr 3. Ale równocześnie a₄ ma metraż 120 metrów kw., zaś a₁ tylko 95 metrów kw. Jeśli próg weta dla odnoszącego się do metrażu kryterium f₃ wynosi v₃ = 20, to znaczy, że różnica pomiędzy f₃(a₄) i f₃(a₁) jest od niego większa, bo wynosi 25. Wówczas przestają nas interesować pozostałe kryteria, w których a₁ wygrywa - uznajemy, że metraż tego wariantu jest po prostu zbyt mały w porównaniu z a₄. Mówimy, że odrzucamy hipotezę o tym, iż a₁ przewyższa a₄. Warianty te są nieporównywalne.

Bardziej wymowny byłby może przykład z szukaniem pracy: posada A jest pod wszelkimi względami (pensja, komfort, stanowisko, możliwości rozwoju itd.) lepsza od posady B. Problem w tym, że siedziba firmy A jest położona dużo, dużo dalej od naszego domu niż siedziba B. Na tyle daleko, iż zakłóca to nasze odruchowe przekonanie, że A całościowo "przewyższa" B - ale też nie możemy powiedzieć, że praca B, ze wszech miar przygnębiająca i niskopłatna, jest "lepsza" tylko dlatego, że mamy do niej blisko. Ostatecznie więc A i B są nieporównywalne.

Zbiór D_v nazywamy zbiorem niezgodności. Trafiają tam te pary a_j, a_i, dla których k-te kryterium wypada w przypadku a_j gorzej niż w przypadku a_i nawet po uwzględnieniu progu weta. Zatem trafi tam np. para (a₁, a₃) z naszej opowieści o nieruchomościach, a także para (A, B) z historii o posadach.

Zauważmy, nawiasem mówiąc, że próg weta formalnie zależy nie tylko od samego kryterium, ale również od wariantu, bo zapis to v_k[f_k(a_j)]. Teoretycznie więc może być tak, że np. trzecia rozważana posada, nazwijmy ją C, będzie miała tak nieprawdopodobne zalety, iż będziemy ją preferowali nawet jeśli trzeba będzie dojeżdżać do niej bardzo długo, pokonując ogromny dystans, np. 150 km w jedną stronę. Tymczasem w przypadku A "odpuścimy" sobie znacznie szybciej, już przy 100 km. Patrząc na czas: możemy np. uznać, że do A gotowi jesteśmy jechać o 30 minut dłużej niż do dowolnej alternatywnej pracy, ale do C - nawet godzinę dłużej.

*

Wróćmy do głównego toru naszych dywagacji. Otóż relacja to - jak wiemy z teorii mnogości - po prostu podzbiór iloczynu kartezjańskiego. Te elementy są ze sobą w relacji, które - wzięte jako pary (a_j, a_i) - należą do tego zbioru. Stąd definicję relacji przewyższania możemy opisać tak:

- przy czym:

Innymi słowy, D_v z nadkreślnikiem to dopełnienie zbioru D_v. A zatem relacja przewyższania polega na spełnieniu równocześnie dwóch sytuacji: zgodności i braku niezgodności (braku).

Można to ująć bardziej intuicyjnie, wprowadzając pojęcia warunku zgodności i warunku braku niezgodności (braku, podkreślmy!). Wyglądają one tak, w podanej kolejności:

A zatem w pierwszym przypadku chcemy, by współczynnik zgodności dla dwóch wariantów przewyższał wartość progową, w drugim - by przynajmniej po uwzględnieniu progu weta wariant a_j był nie gorszy niż a_i (w świetle każdego kryterium).

Współczynnik zgodności, dodajmy, mówi o tym, jak istotne są te kryteria, na których a_j prezentuje się nie gorzej niż a_i.

To, że mamy dwa warunki, jest ważne. Może być bowiem tak, że wariant a_j według żadnego z kryteriów "nie oddala się" od a_i o więcej niż próg weta, ale z drugiej strony faktycznie przewyższa a_i tylko na jakichś bardzo mało istotnych kryteriach - przez co współczynnik zgodności c(a_j, a_i) jest mniejszy niż żądany próg s.

Na przykład: samochód marki X, którego kupno rozważamy, co prawda w żadnym wypadku nie jest tragicznie gorszy niż pojazd marki Y, ale o tym, że być może jest lepszy, możemy powiedzieć tylko dlatego, że ma elegancko zdobioną dźwignię zmiany biegów. A to przecież nie jest (chyba...) szczególnie istotne kryterium. To nie wystarczy, by wybrać X. Owszem, w czymś góruje nad Y, a w dodatku nie jest od niego wyraźnie słabszy w przyspieszeniu czy zużyciu paliwa, ale to "górowanie" jest zbyt mało ważne z naszego punktu widzenia. Tak więc X nie przewyższa Y.

*

Dodajmy małe usprawnienie matematyczne. Otóż dotychczas zakładaliśmy, że wagi w_k są dowolnymi liczbami rzeczywistami. Prościej będzie przyjąć następującą definicję:

To znaczy, że każda waga jest ułamkiem z zakresu [0, 1], przy czym łącznie ich suma to właśnie 1. Na przykład w₁ = 1/5, w₂ = 2/3 itd. Wagi dzielą między siebie tort w postaci jedynki.

Wówczas:

- przy czym:

Wzory te są łatwe do zrozumienia. Dla nas ważniejsza jest uwaga, do której czytelnik być może sam już doszedł: otóż relacja przewyższania, tj. relacja S, nie jest zupełna (spójna). To znaczy, że nie każde dwa warianty w naszej puli są porównywalne. Nie zawsze możemy powiedzieć, że a_j przewyższa a_i lub a_i przewyższa a_j. Oczywiście może tak być, tym lepiej dla nas, ale jeżeli ten szczęśliwy traf się nie zdarzy, to metoda ELECTRE pomoże nam jedynie w uformowaniu pewnego zestawu "potencjalnie dobrych" scenariuszy, które możemy dalej analizować. Będziemy np. wiedzieć, że nieruchomości 3 i 4 przewyższają swymi cechami nieruchomości 1, 2 i 5 - ale nie będzie jasne, czy "trójka" jest lepsza od "czwórki" lub odwrotnie.


Adam Witczak

BIBLIOGRAFIA:

J. Michnik, "Wielokryterialne metody wspomagania decyzji", Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2013

M. Nowak, "Metody ELECTRE w deterministycznych i stochastycznych problemach decyzyjnych", Decyzje nr 2, grudzień 2004

T. Trzaskalik, "Wielokryterialne wspomaganie decyzji. Przegląd metod i zastosowań", Zeszyty Naukowe Politechniki Śląskiej, seria: Organizacja i Zarządzanie, zeszyt 74, 2014.