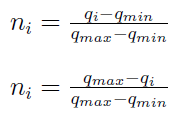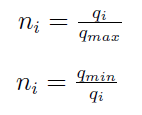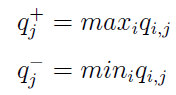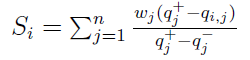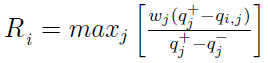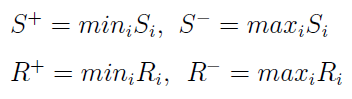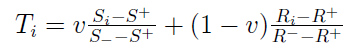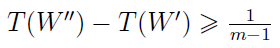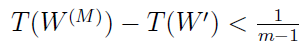VIKOR i wielokryterialne wspomaganie decyzji

VIKOR to jedna z metod wielokryterialnej optymalizacji decyzji. Podobnie jak TMAI czy TOPSIS, oparta jest na koncepcji mierzenia odległości badanego wariantu od scenariusza idealnego. Tego pomiaru dokonuje się przy pomocy trzech metryk, a później rozważa się jeszcze dodatkowe warunki.

Technikę VIKOR opracował jugosławiański (serbski) matematyk Serafim Opricovic. Był to przedmiot jego pracy doktorskiej, obronionej w roku 1979. Nazwa jest pewnego rodzaju skrótem, a rozwija się ją następująco: VIseKriterijumska Optimizacija I Kompromisno Resenje.

Działanie tej metody przedstawimy w ślad za publikacjami wymienionymi w bibliografii. W zasadzie nie będziemy wnikać głębiej w motywację tego podejścia czy też w uzasadnienie optymalności generowanych wyników. Po prostu wykraczałoby to poza ramy tekstu. W każdym razie metoda jest powszechnie akceptowana w kręgu osób badających i wykorzystujących narzędzia MCDM (multi-criteria decision making).

Załóżmy, że mamy n kryteriów indeksowanych literą j. Na przykład w przypadku inwestycji w nieruchomości takimi kryteriami mogą być powierzchnia, cena metra kwadratowego, stan techniczny (o ile da się go określić przy pomocy punktów), odległość od pewnego ustalonego punktu etc. W przypadku spółki giełdowej badać można rentowność netto, płynność bieżącą czy zadłużenie w relacji do sumy bilansowej.

Każde kryterium ma swoją wagę w_j. Wagi te mogą być różne (możemy przecież uważać, że cena metra kwadratowego jest ważniejsza niż wiek budynku lub odwrotnie), zasadniczo jednak powinny sumować się do liczby 1. Na przykład 0.5, 0.25, 0.15 i 0.10 dla czterech kryteriów.  

Warianty (czyli właśnie nasze spółki lub nieruchomości) indeksujemy literką i. Możemy przyjąć, że jest ich łącznie m.

Przez q_i,j oznaczać będziemy ocenę i-tego wariantu w świetle j-tego kryterium. Na przykład rentowność netto trzeciej spółki. Tak naprawdę zakładamy, że oceny te są znormalizowane, sprowadzone do tego samego rzędu, w szczególności do zakresu [0, 1]. Można to osiągnąć na różne sposoby. Prezentujemy dwa z nich:

Normalizacja typu 1)

Pierwszy wiersz odnosi się do stymulant, tj. do zmiennych, co do których pożądane są wysokie wartości. Stymulantą jest rentowność netto (chcemy jak najwyższej). Destymulanty to zmienne, które są najlepsze, gdy są najniższe. Przykładem (choć to bardzo uproszczone ujęcie) może być zadłużenie.

Normalizacja typu 2)

Ta normalizacja jest jeszcze prostsza od poprzedniej. Dla stymulant bierzemy stosunek badanej wartości do najlepszej w świetle danego kryterium. Na przykład dzielimy rentowność spółki przez najlepszą rentowność w całym portfelu. I tak dla każdego podmiotu. W przypadku destymulant wzór też jest zrozumiały.

Przejdźmy do rzeczy, do VIKOR. W pierwszym kroku określamy dla każdego kryterium najlepszą i najgorszą wartość, odpowiednio q_j⁺ i q_j^-:

Tutaj nie przejmujemy się już podziałem na stymulanty i destymulanty. Jesteśmy po normalizacji: każda wartość jest teraz dobra, gdy jest wysoka - i kiepska, gdy niska.

Obliczamy dla każdego wariantu metryki S oraz R. Nawiasem mówiąc, czytelnik powinien uważać na tego rodzaju niuanse: czy w danym momencie idziemy po kolejnych wariantach (scenariuszach), czy po kolejnych kryteriach. Tu - po wariantach:

Wzory te na pierwszy rzut oka mogą się wydawać skomplikowane, wystarczy jednak przyjrzeć im się przez chwilę, by przekonać się, że nie są aż takie straszne. Zgodnie jednak z wcześniejszą zapowiedzią, nie będziemy wchodzić w takie rozważania, szczególnie że trudno tu o cokolwiek mądrzejszego niż prześledzenie krok po kroku, jak formuła jest liczona. Zauważmy jedynie, że w mianownikach ułamków mamy różnicę pomiędzy najlepszym i najgorszym wynikiem dla ustalonego kryterium. W liczniku jest z kolei różnica pomiędzy rezultatem najlepszym, a tym, który akurat badamy (czyli dla i-tego wariantu).

Im mniejsze wartości S_i R_i, tym dany scenariusz lepszy - łatwo to zauważyć (bliższy ideałowi).

W następnym kroku wyliczamy następujące wartości:

Do czego są nam one potrzebne? Stosujemy je w kolejnej, trzeciej już metryce. Ma ona nazwę T:

Jak widać, znów liczymy jej wartości dla każdego (i-tego) scenariusza. Pojawia się tu liczba v, którą np. A. Kobryń określa jako "wagę odzwierciedlającą ważność strategii większości kryteriów". Z kolei 1 - v to tzw. siła weta. Mówiąc inaczej, za J. Michnikiem, v reprezentuje znaczenie ważonej sumy kryteriów, a 1 - v oddaje znaczenie najsłabszego kryterium.

Rzecz dotyczy sytuacji, w których dany wariant w zasadzie okazuje się zadowalający, najlepszy ze wszystkich, ale w świetle jednego z kryteriów zawodzi w sposób tak bardzo niedopuszczalny, że powoduje odrzucenie tej propozycji.

Jeśli preferujemy zawsze wybór większościowy, tj. akceptujemy ten wariant, który ma najlepsze wyniki w świetle największej liczby kryteriów, to przyjmujemy v > 0.5. Gdy v = 0.5, to jest to preferowanie konsensusu. Często tak właśnie się przyjmuje. Gdy v < 0.5, to jest to wybór z wetem.

Znów: lepsze warianty mają niższe wartości T. Ale wartości S, R i T to nie wszystko. Możemy na ich podstawie utworzyć trzy listy rankingowe w porządku rosnącym, czyli od najmniejszych (najlepszych zarazem) wyników do najwyższych (najgorszych). To jest następny krok VIKOR.

Szukamy teraz rozwiązania kompromisowego. Jak to się robi? Na początek interesuje nas minimum z metryki T. Szukamy zatem tego i-tego wariantu, dla którego T_i jest najniższe. Ale uwaga: musimy sprawdzić jeszcze dwa warunki:

C1) To warunek "akceptowalnej przewagi":

Przez W'' rozumiemy drugą pozycję na liście rankingowej według metryki T. Czyli ten scenariusz, który w świetle T jest tylko trochę gorszy niż najlepszy, jest zaraz po nim. Z kolei m to liczba wariantów. W' to nasz wstępnie najlepszy scenariusz, tak więc T(W') to minimalne T_i.

C2) Ten warunek to tzw. "akceptowalna stabilność". Chodzi o to, że nasz wstępny najlepszy wariant W' powinien być wiodący nie tylko według metryki T, ale też S lub R (zauważmy, że chodzi o spójnik "lub", nie wymaga się, by wiódł prym według obu tych metryk).

Załóżmy, że przynajmniej jeden z tych warunków nie jest spełniony. Przyjmijmy wpierw, że zawodzi tylko C2. Wtedy za kompromisowe rozwiązanie uważamy zbiór zawierający W' i W''. Cóż, pozostajemy z dwoma najlepszymi rozwiązaniami i musimy szukać innych metod ich dookreślenia.

Jeśli nie jest spełniony warunek C1, to za kompromisowy uważamy zbiór alternatyw W', W'', ..., W^(M), przy czym:

Innymi słowy, bierzemy takie scenariusze, że pod względem metryki T różnią się one od W' o mniej niż 1/(m-1).

Pewnym tropem do zrozumienia metryk S i R oraz całej metody jest uwaga poczyniona przez A. Kobrynia, iż rozwiązanie kompromisowe, wygenerowane metodą VIKOR, "zapewnia maksymalną użyteczność grupową (reprezentowaną przez min S) oraz minimalny sprzeciw oponentów (reprezentowany przez min R)".

Metoda VIKOR ma rozmaite warianty, m.in. oparte o teorię zbiorów rozmytych. Swój autorski wariant przedstawił też polski naukowiec J. Michnik - i jest to metoda VIKOR-S, która prowadzi nie do zbioru rozwiązań kompromisowych, lecz zawsze do najlepszego wariantu.

Tyle teorii - ale prezentujemy też osobne opracowanie, w którym testujemy metodę VIKOR na czterech przedsiębiorstwach z warszawskiej GPW.


Adam Witczak

BIBLIOGRAFIA:

B. Bulgurcu, "Investment Destination Decision by Using the VIKOR Method in the European Union Countries", American International Journal of Contemporary Research, vol. 6, no. 2, April 2016.

C. Dominiak, "Wielokryterialne wspomaganie podejmowania decyzji strategicznych w przedsiębiorstwie", Wyd. Uniwersytetu Ekonomicznego w Katowicach 2013.

A. Kobryń, "Wielokryterialne wspomaganie decyzji w gospodarowaniu przestrzenią", Difin 2014.

M. Koray, E. Ipekci, "Multi-criteria analysis of banks' performances", International Journal of Economics and Finance Studies, vol. 2, no. 2, 2010.

J. Michnik, "Wielokryterialne metody wspomagania decyzji w procesie innowacji", Wyd. Uniwersytetu Ekonomicznego w Katowicach 2013.