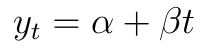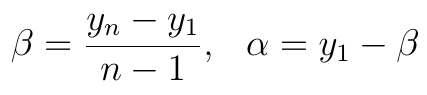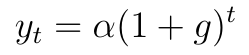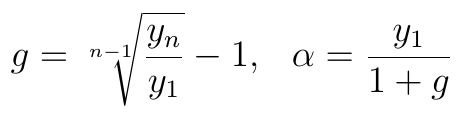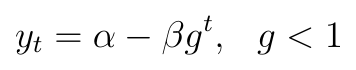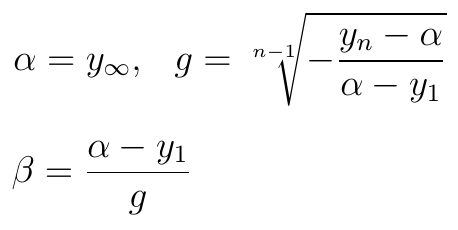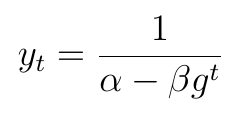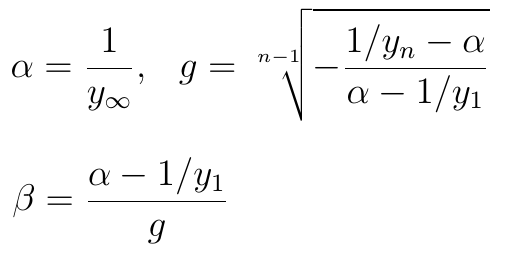Od prognoz liniowych do logistycznych

Funkcje, o których będziemy mówić, znajdują bardzo szerokie zastosowanie w matematyce wszelkiego rodzaju, w szczególności zaś w finansach i ekonomii. My możemy myśleć o nich na przykład jako o narzędziach pomocnych przy modelowaniu trendu, według którego rosną przychody ze sprzedaży, generowane przez przedsiębiorstwo.

Oczywiście chodzi tu o prognozowanie. Na podstawie danych z poprzednich okresów (np. z minionych lat) analityk próbuje niejako domyślić się ogólnej tendencji, a następnie chce przybliżyć ją przy pomocy funkcji.

Zagadnienie to jest rzecz jasna bardzo złożone i poświęca mu się liczne prace naukowe, ale podstawowe, najczęściej stosowane typy funkcji są relatywnie proste i jest ich tylko kilka.

Po pierwsze, możemy stosować funkcje liniowe:

Otóż przychody, określone tu przez y, rosną (albo spadają, to wariant pesymistyczny) w taki sposób, że wykres kwot w poszczególnych momentach układa się, jeśli połączyć punkty, jak linia prosta (czy też półprosta, bo startujemy z jakiegoś miejsca - lub jak odcinek, bo gdzieś możemy nasze przewidywania zakończyć).

Zmienna t mierzy oczywiście czas i tak naprawdę jest dyskretna, ale dla celów teoretycznych można ją postrzegać jako ciągłą. Model ma dwa parametry: α i β. Oblicza się je na podstawie dostępnych danych empirycznych:

Jak widać, chcąc znać beta, rozważamy znane nam skądinąd przychody z roku początkowego i pewnego, też już minionego, roku późniejszego (np. z lat 2015 i 2016, albo 2000 i 2005). Odejmujemy starsze obroty od nowszych i dzielimy wynik przez n-1. Współczynnik kierunkowy to różnica pomiędzy przychodami pierwszego rozpatrywanego roku a parametrem β.

Bardziej złożony model oparty jest o funkcję wykładniczą:

Wzór ten przypomina formułę procentu składanego. Rzeczywiście, liczbę g nazywamy stopą wzrostu. Z kolei α to punkt, z którego nasza krzywa startuje. Parametry te kalkuluje się tak:

Jak widać, stopę wzrostu liczymy przy użyciu wzoru powiązanego ze średnią geometryczną, o której pisaliśmy przy okazji analizowania indeksów statystycznych.

Funkcję wykładniczą można trochę zmodyfikować - w taki sposób, by miała asymptotę poziomą:

Zauważmy, że teraz oczekujemy, iż g będzie mniejsza niż 1. Parametry liczy się następująco:

Otóż α to pewna ustalona przez nas liczba: prosta wyznaczająca asymptotę wykresu funkcji. Takie ujęcie ma sens. Naturalne wydaje się bowiem założenie, że nawet przychody bardzo dobrej i dużej firmy w pewnym momencie de facto przestaną rosnąć (nawet jeżeli formalnie wciąż będą się zwiększać, to jednak dynamika będzie już bardzo skromna). Tymczasem modele liniowy i wykładniczy (zwykły) zakładają, że obrót będzie się zwiększał i zwiększał, od milionów do miliardów - i któż wie, dokąd potem...

Ostatni model, o którym wspomnimy, to model logistyczny. Formuła funkcji jest następująca:

Znów mamy tu do czynienia z asymptotą. Parametry określone są poniższymi wzorami:

O funkcji logistycznej pisaliśmy więcej w odrębnym artykule. Trend logistyczny pasuje on do modelowania sytuacji, w których rozważana wielkość (np. przychody) najpierw rośnie szybko, później tempo tego wzrostu słabnie, a na końcu funkcja się stabilizuje, tzn. co prawda wciąż rośnie, ale zbliża się do asymptoty poziomej, nigdy jej wszelako nie osiągając.

Funkcji logistycznej używa się m.in. przy budowie jednego z modelu wzrostu dywidendy wypłacanej przez spółkę akcyjną. Metodę taką przedstawił J. B. Williams w pracy The Theory of Investment Value, wydanej w roku 1956.

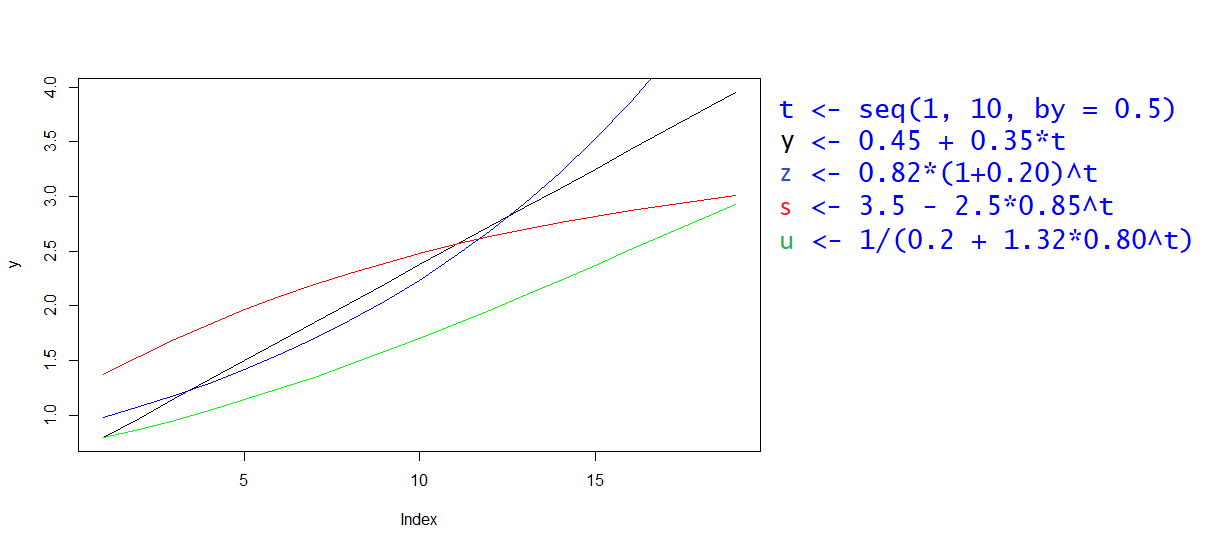
My tymczasem spójrzmy na wykresy przykładowych funkcji - po jednej z każdej omawianej przez nas rodziny:

Zmienna t to oczywiście czas, oś odciętych. Funkcja y, o czarnym wykresie, to pewna funkcja liniowa. Niebieski wykres to z - funkcja wykładnicza. Na czerwono mamy s - funkcję wykładniczą zmodyfikowaną, wyposażoną w asymptotę poziomą. Wreszcie jest i pewna funkcja logistyczna u, zaznaczona na zielono. Parametry są dobrane dość arbitralnie, bo nie chodziło nam o jakieś szczególne badania nad tymi konkretnymi przykładami.

Opisane przez nas narzędzia nie są, jak zresztą daliśmy uprzednio do zrozumienia, jedynymi, które się rozważa przy modelowaniu przychodów, a tym bardziej - innych zjawisk ekonomicznych. Popularne są też np. funkcje Toernquista (w trzech wariantach) czy funkcja hiperboliczna.


Adam Witczak

BIBLIOGRAFIA:

P. Dittmann, E. Szabela-Pasierbińska, I. Dittmann, A. Szpulak, "Prognozowanie w zarządzaniu sprzedażą i finansami przedsiębiorstwa", Wolters Kluwer Polska 2011.

P. Dittmann, "Prognozowanie na podstawie szeregów czasowych", w: "Prognozowanie gospodarcze. Metody i zastosowanie", praca zbiorowa pod red. M. Cieślak, PWN 2001.

A. Ganczarek-Gamrot, "Analiza szeregów czasowych", Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2014

K. Pera, R. Buła, D. Mitrenga, Modele inwestycyjne, C. H. Beck, Warszawa 2014.