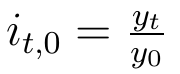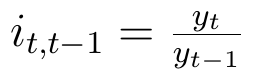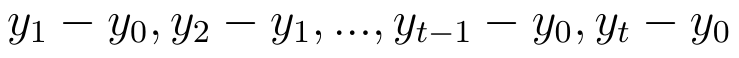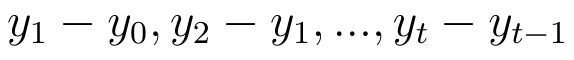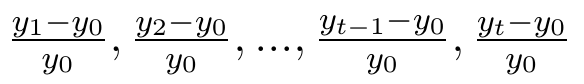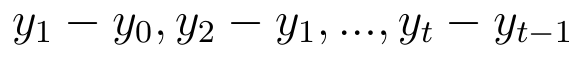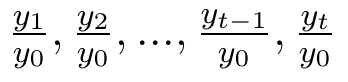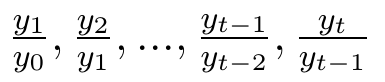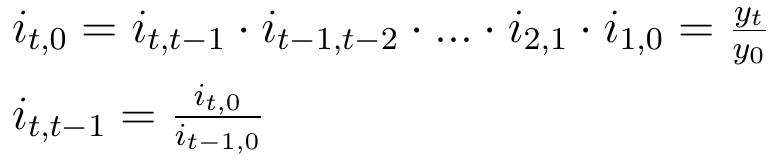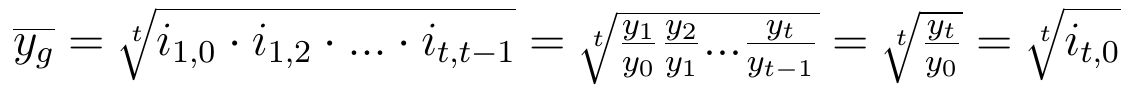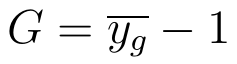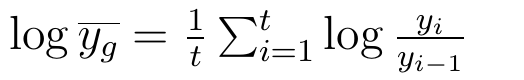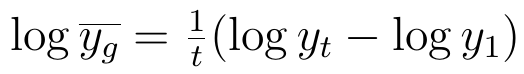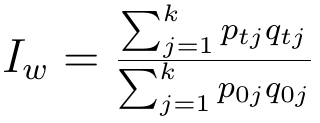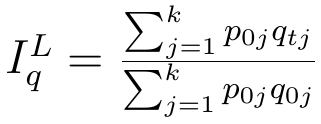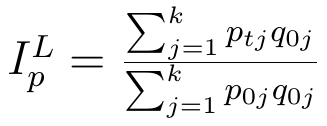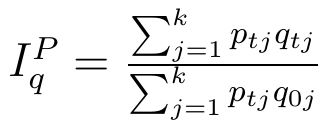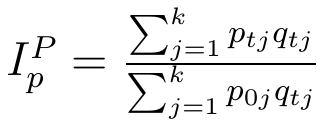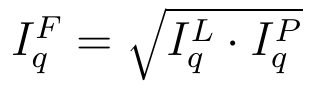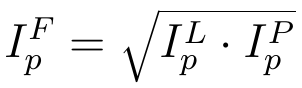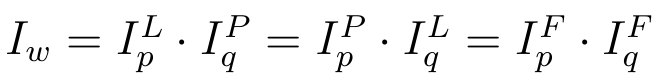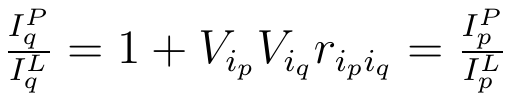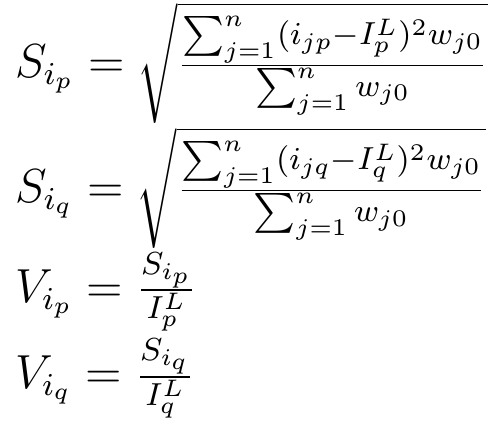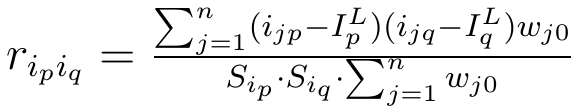Indeksy statystyczne

Indeksy statystyczne to grupa narzędzi (formuł matematycznych), przy pomocy których bada się dynamikę zjawisk w czasie. Najprościej rzecz ujmując, taki indeks to stosunek wielkości danego zjawiska w badanym momencie (okresie) do jego wielkości w pewnym momencie przyjętym jako podstawowy czy też wyjściowy. Ta druga chwila jest zazwyczaj umiejscowiona w przeszłości, w każdym razie takie ujęcie wypada uznać za najbardziej sensowne i naturalne.

Indeksy klasyfikuje się według różnych kryteriów. Na przykład można mówić o indeksach indywidualnych i agregatowych (zespołowych). Zacznijmy od tych pierwszych.

Otóż indeksy indywidualne stosuje się w odniesieniu do zjawisk jednorodnych. Przy ich pomocy możemy np. określić roczną dynamikę wzrostu (lub spadku) populacji w Polsce - albo miesięczną dynamikę ceny mleka w skupie.

Od razu trzeba rzec, iż indeksy indywidualne mogą być jednopodstawowe lub łańcuchowe. Wzór jednopodstawowy wygląda tak:

Nie jest to specjalnie odkrywcze. Jak widać, wielkość y w momencie t (czyli y_t) dzielimy przez wielkość y w chwili zerowej. Mianownik jest ustalony, niezależny od t. W ten sposób możemy mówić np. o rocznej, dwuletniej czy pięcioletniej dynamice ludności.

Podstawa może jednak zmieniać się, a konkretniej - rosnąć. Na ogół będzie jeden krok poniżej czasu aktualnego. W ten sposób otrzymujemy indeks łańcuchowy:

Jak widać, tym razem np. rok trzeci porównujemy z drugim, siódmy z szóstym itd. Teoretycznie można sobie wyobrazić także skoki dwuletnie czy nawet wieloletnie. Wówczas rozpatrywalibyśmy i_t,t-k określone jako y_t / y_t-k, gdzie k nie powinno przekraczać t. Zasadniczo jednak nie będziemy rozpatrywać takiego modelu.

W nawiązaniu do koncepcji indeksów możemy też rozpatrywać bezwzględne przyrosty jednopodstawowe:

...i łańcuchowe:

To były przyrosty bezwzględne. Na przykład jeśli y określa ludność Polski w wieku produkcyjnym, to y₁₉₉₁ - y₁₉₉₀ wynosi 21,5 mln - 21,9 mln = -0,4 mln (osób). Znowuż y₁₉₉₃ - y₁₉₉₀ = 22 mln - 21,9 mln = 0,1 mln. Tak się składa, że tyle samo wynosi y₁₉₉₃ - y₁₉₉₂.  

A oto przyrosty względne:

- jednopodstawowe:

- łańcuchowe:

Wróćmy do indeksów. Tu również można mówić o ciągach:

- indeksów jednopodstawowych:

- łańcuchowych:

Zaprezentowane dotychczas wzory nie są specjalnie ambitne. W praktyce zresztą często używamy ich niemal bezwiednie przy różnych okazjach ("nie wiedząc, że mówimy prozą"). Rozważmy zatem nieco bardziej skomplikowane zagadnienia.

Po pierwsze, indeksy łańcuchowe można zamieniać na jednopodstawowe, a jednopodstawowe na łańcuchowe. Obrazują to poniższe formuły:

Po drugie, możemy pomyśleć o przeciętnym tempie zmian w dłuższym przedziale czasowym, w którym mamy np. kilka czy kilkanaście momentów analizy. Oczywiście pojęcie "średniej" czy "przeciętnej" jest wieloznaczne: można sobie wyobrazić na przykład średnią arytmetyczną z kilku dynamik rocznych. W obszarze, który dziś omawiamy, stosuje się jednak raczej średnią geometryczną. Jest to pierwiastek stopnia t z iloczynu t wyrażeń (zauważmy, że w takim razie samych momentów w czasie jest t+1, od zerowego do t-tego):

Okazuje się, że tak naprawdę liczą się tu tylko dwie wielkości: ostatnia i pierwsza. Przeciętne tempo zmian wyraża się następującą formułą:

Rozważmy np. kursy zamknięcia akcji spółki Kompap na GPW z 14 sesji (takich, w czasie których generowano jakiś obrót papierami tej firmy), od 15 czerwca do 24 lipca 2018:

8.10, 8.00, 7.85, 7.85, 7.80, 7.85, 7.50, 7.50, 7.25, 7.40, 7.75, 7.75, 8.00, 7.20 (zł).

Średnia geometryczna z odpowiednich indeksów łańcuchowych (nie z samych cen!) to pierwiastek 13. stopnia (bo 14 kursów daje nam 13 indeksów) z 7.20 / 8.10. Ten zaś wynosi, jak możemy policzyć np. w pakiecie R, dokładnie 0.9909807. Jeśli odejmiemy 1 od tej liczby, to dostaniemy -0.0090193, czyli ok. -0,9 proc. A więc "średnio" kurs akcji malał z sesji na sesję o 0,9 proc. w badanym okresie.

Jeśli badany szereg czasowy składa się z wielu wyrazów, to obliczenia można uprościć, stosując logarytmy. Wzór na średnią geometryczną logarytmuje się tak:

Biorąc pod uwagę ostateczną jego postać, uwzględniającą tylko momenty 0 i t, możemy napisać:

***

Bardziej zaawansowane zagadnienie to indeksy agregatowe. Dotyczą one zjawisk niejednorodnych. Na przykład mamy pakiet produktów różnego rodzaju (jabłka, gruszki, banany - albo nawet jabłka, zapałki i długopisy), każdy produkt ma w dodatku inną cenę jednostkową. Agregaty stosowane w profesjonalnej makroekonomii to np. PKB, produkcja przemysłowa, eksport czy sprzedaż detaliczna.

Czy można mówić o dynamice wartości takich agregatów? Owszem, da się to zrobić przynajmniej na kilka sensownych sposobów.

Zacznijmy od indeksu wartości:

Oznaczenia są następujące:

k - liczba artykułów (np. gatunków owoców)

p_tj - cena j-tego artykułu w okresie t, p_0j - cena j-tego artykułu w okresie bazowym

q_tj - ilość j-tego artykułu w okresie t, q_0j - ilość j-tego artykułu w okresie bazowym

Indeks mówi nam, jak (o ile) zmieniła się zmieniła się wartość rozważanych artykułów w badanym okresie w relacji do bazowego. Pojedynczy składnik każdej sumy to iloczyn ceny i ilości, zatem wartość pojedynczego artykułu.

Otóż właśnie cena i ilość wpływają na ostateczny rezultat. Z tego względu stosuje się tzw. standaryzację indeksów agregatowych. To znaczy, że przyjmuje się, iż albo ceny, albo ilości były stałe w obu okresach. Jeden z tych czynników jest zatem ustalany.

Stałe - czyli takie jak w czasie bazowym, czy takie jak w aktualnym? Można zastosować jedno i drugie podejście. W pierwszym wypadku korzystamy z metody Laspeyresa. W ten sposób powstają poniższe formuły (pierwsza to indeks ilości przy ustalonych cenach, druga to indeks cen przy ustalonych ilościach):

Druga koncepcja to formuły Paaschego:

Tutaj przyjęto ceny lub ilości z okresu badanego. Okazuje się zresztą, że wyniki Laspeyeresa i Paaschego różnią się od siebie, ale o tym - za parę chwil.

Co właściwie pokazują nam te indeksy? Ilościowe mówią nam, jaki wpływ na zmianę wartości agregatu miałaby sama tylko zmiana ilości przy założeniu stałych cen. Cenowe mówią, jaki wpływ na modyfikację wartości agregatu miałaby sama tylko zmiana cen - przy przyjęciu, że ilość towarów byłaby taka sama.

Wyobraźmy sobie teraz, że mamy następującą tabelkę:

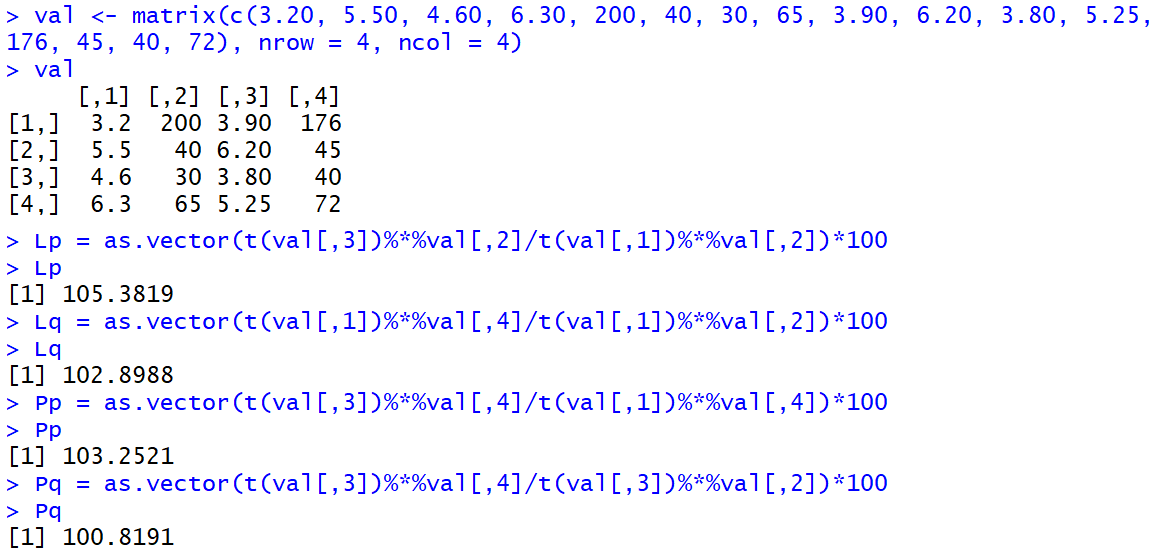
Powiedzmy, że tabela ta opisuje spożycie owoców w jakiejś małej wspólnocie (np. rodzinie). Tak naprawdę dane, w tym ceny, są obmyślone na poczekaniu - ale nie o realizm nam w tym momencie chodzi. Obliczmy indeksy ilościowe i cenowe w obu wersjach (Laspeyeresa i Paaschego), posługując się językiem R (adaptujemy funkcje opracowane przez p. M. R. Meyera i zamieszczone na witrynie prof. R. N. Fernandeza):

Przeanalizujmy pokrótce ten kod. Otóż mnemotechnicznie można to przyswoić przy pomocy następujących zależności:

- Laspeyres cenowy: (nowa cena * stara ilość) / (stara cena * stara ilość)

- Laspeyres ilościowy: (stara cena * nowa ilość) / (stara cena * stara ilość)

- Paasche cenowy: (nowa cena * nowa ilość) / (stara cena * nowa ilość)

- Paasche ilościowy: (nowa cena * nowa ilość) / (nowa cena * stara ilość)

Widzimy, że np. indeks cenowy Laspeyeresa wynosi w przybliżeniu 105,38 (proc.). To znaczy, że gdyby ilości w roku 2016 pozostały takie jak 2015, to wzrost wydatków byłby skutkiem zwyżki cen o 5,38 proc. Gdyby przyjąć ilości z roku 2016, to wzrost wartości byłby skutkiem zwyżki cen o 3,25 proc. (formuła Paaschego, tj. Pp = 103,25 proc. w przybliżeniu).

Gdyby ceny pozostały w 2016 takie jak w 2015, a zmieniały się jedynie ilości, to wielkość ogólnych wydatków zwiększyłaby się z powodu wzrostu ilości w kilogramach o 2,9 proc. (formuła Laspeyresa - Lq). Jeżeli ceny byłyby w obu okresach na poziomie roku 2016, to ilość musiałaby średnio wzrosnąć o 0,82 proc.

Jak już mówiliśmy, formuły Laspeyresa i Paaschego dają w zasadzie różne wyniki. Stąd też pojawił się pomysł, by mnożyć te rezultaty przez siebie i brać pierwiastek. W ten sposób powstały indeksy Fishera:

- ilościowy:

- cenowy:

Są to więc średnie geometryczne z indeksów L i P. Obliczmy je dla naszych danych:

Indeks Fishera w pewien sposób (trochę arbitralny, jak to zwykle w ekonometrii i statystyce) "uśrednia" wcześniejsze rezultaty. I tak wychodzi nam, że cena badanych towarów średnio wzrosła o 4,31 proc., a ilość o 1,85 proc. Te liczby mieszczą się pomiędzy odpowiednimi wartościami L i P.

*

Następny wzór podaje nam związki pomiędzy omawianymi indeksami cen, ilości i wartości:

Skąd biorą się różnice pomiędzy indeksami Laspeyresa i Paaschego? Łatwo powiedzieć: z tego, które ceny (resp. ilości) bierzemy. Ale czy można te różnice skwantyfikować bardziej precyzyjnie, uzależnić je np. od rozproszenia danych czy innych parametrów statystycznych?

Otóż zależność tę opisuje formuła zaproponowana przez L. Bortkiewicza:

Oczywiście musimy wyjaśnić oznaczenia. Odpowiednie wzory prezentują się następująco:

A także:

Wielkości V_ip oraz V_iq to współczynniki zmienności indywidualnych indeksów cen i ilości. Z kolei r_ipiq to współczynnik korelacji liniowej Pearsona między tymiż indywidualnymi indeksami. Warto zauważyć, że S_ip oraz S_iq to formuły, które w swej konstrukcji przypominają odchylenie standrdowe. Różnica jest taka, że: - w miejscu średniej mamy indeks Laspeyresa (odpowiednio cenowy i ilościowy); każdy kwadrat różnicy indeksu indywidualnego i agregatowego mnożymy jeszcze przez w_j0, tj. wartość indywidualną j-tego artykułu w okresie bazowym; - a sumę takich przemnożonych kwadratów dzielimy jeszcze przez sumę tychże wartości.

Adam Witczak


BIBLIOGRAFIA:

"Wspomaganie procesów decyzyjnych. Tom I. Statystyka", pod red. M. Lipiec-Zajchowskiej, C.H. Beck 2003.

T. Michalski, "Statystyka", WSiP 1999.

M. Sobczyk, "Statystyka. Podstawy teoretyczne, przykłady, zadania", Wydawnictwo UMCS 2000.

"Metody statystyczne w zarządzaniu", pod red. D. Witkowskiej, Wydział Organizacji i Zarządzania Politechniki Łódzkiej 1999.