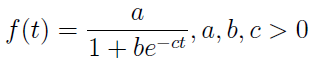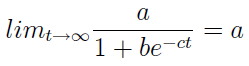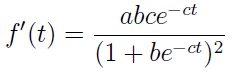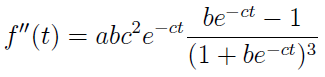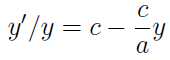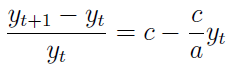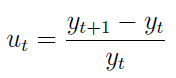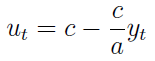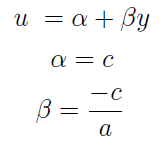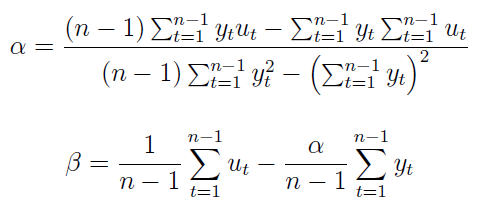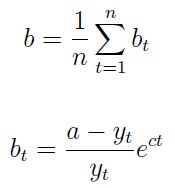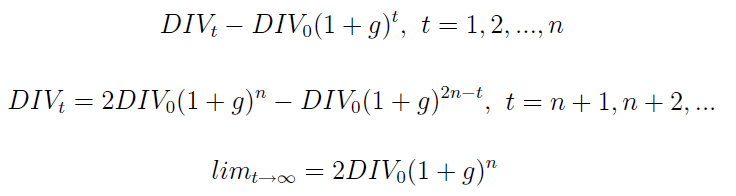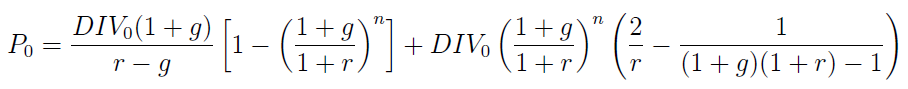Funkcja logistyczna i dywidenda

Swego czasu – przy okazji rozważań nad kanałami i wstęgami na wykresach kursów akcji – omówiliśmy regresję liniową w oparciu o metodę najmniejszych kwadratów i szukanie przy jej pomocy linii prostej, która najlepiej przybliżałaby trend zauważalny w danych empirycznych.

Wzorów tych nie będziemy tu powtarzać, albowiem przedmiotem naszego zainteresowania będzie inna sytuacja – taka mianowicie, gdy trend liniowy nie oddaje zbyt dobrze zmian badanego zjawiska. Wystarczy, że przyrosty analizowanej wielkości nie będą w przybliżeniu stałe w kolejnych (równych sobie) jednostkach czasu – i już może pojawić się problem.

Wtedy trzeba szukać innych krzywych, przy czym często okazuje się, że dobrym wyborem jest tzw. trend logistyczny. Pasuje on do sytuacji, w których dana wielkość najpierw rośnie intensywnie (szybko), ale później tempo tego wzrostu słabnie, a ostatecznie dochodzi do względnej stabilizacji.

Z takim scenariuszem stykamy się w ekonomii, badając popyt na niektóre dobra, zwłaszcza dobra trwałego użytku, równocześnie mające w sobie aspekt nowości (na przykład technologicznej). Mówiąc w dużym uproszczeniu, z początku wszyscy chcą mieć tak niezwykły wynalazek jak telewizor, ale kiedy dotrze on już do (prawie) wszystkich gospodarstw domowych, to nieraz służy całe lata, potrzeby zakupowe w skali ogólnorynkowej maleją i przyrost liczby urządzeń hamuje.

Oto wzór krzywej, która opisuje to zjawisko, czyli krzywej logistycznej:

Naturalnie a, b, c to pewne parametry, które należy dopasować np. na podstawie dociekań empirycznych. Jako dziedzinę funkcji przyjmuje się przedział od zera do nieskończoności (tzn. nieujemne liczby rzeczywiste). Wykres tejże funkcji przecinać będzie się z osią rzędnych (tj. OY) w punkcie (0, a / (1+b)). Funkcja ta w nieskończoności będzie ograniczona przez liczbę a, tzn.:

Wykres funkcji będzie miał więc asymptotę poziomą według równania y = a, przy czym wartość a nie będzie osiągana, choć będzie można zbliżyć się do niej dowolnie blisko. Parametr a określa się mianem poziomu nasycenia krzywej logistycznej.

Można pokazać, że funkcja ta jest w całej swej dziedzinie monotoniczna, a konkretniej – rosnąca. Wynika to np. z następującego rozpisania, w którym korzystamy z pochodnej pierwszego rzędu:

Jak widać, w mianowniku mamy kwadrat liczby dodatniej, licznik również jest liczbą dodatnią, biorąc pod uwagę założenia przyjęte co do a, b, c.

Można też sprawdzić, w którym zakresie zmiennych funkcja jest wypukła, a w którym wklęsła. W tym celu oblicza się drugą pochodną (pominiemy obliczenia, które trzeba zrealizować po drodze):

Jeśli zbadamy znak tejże drugiej pochodnej, to okaże się, że mamy wypukłość dla t należących do [0, ln(b) / c) oraz wklęsłość na prawo od ln(b) / c. Sam ten punkt ma charakter krytyczny, jest to punkt przegięcia, w którym funkcja osiąga wartość a / 2.

Pokażemy teraz, jak wyznacza się – tzw. metodą Hottelinga – parametry krzywej logistycznej na podstawie danych empirycznych. Krzywa ta nie jest dana funkcją liniową, jak już wiemy, niemniej określone przekształcenia matematyczne pozwalają na przedstawienie jej w takiej postaci.

Oto bowiem okazuje się, że pochodną badanej funkcji zapisać można tak:

To równanie można jednak przybliżyć dzięki własnościom różniczki funkcji, a dzięki temu zastąpić równaniem różnicowym (w miejsce różniczkowego – to istotna różnica!):

Zmienna t przebiega tu wartości naturalne od 1 do n-1, gdzie n to liczba empirycznych pomiarów, jakimi dysponujemy. Wartości tych pomiarów dla kolejnych jednostek czasu to y₁, y₂, … , y_n. W istocie jednak w opisywanej metodzie będziemy bezpośrednio wykorzystywać inne wartości, mianowicie względne przyrosty analizowanej wielkości:

Ale prawą stronę już znamy. Możemy zatem zapisać:

Tę wersję można jeszcze bardziej uogólnić:

To już niewątpliwie jest funkcja liniowa. Tym samym parametry α, β można obliczyć np. metodą najmniejszych kwadratów – mniej więcej tak, jak to przedstawiono we wspomnianym wcześniej naszym poprzednim tekście.

Tutaj konkretne wzory przyjmą następującą postać:

Znając powyższe wartości, możemy wrócić do współczynników a oraz c funkcji logistycznej (czyli w pewnym sensie wycofujemy się z liniowości). A co dzieje się z b? Otóż przyjmujemy:

A zatem naszym b będzie średnia arytmetyczna z wartości b_t wyliczonych na podstawie danych empirycznych y_t. Wynika to z faktu, że suma kwadratów odchyleń pomiędzy b i b_t powinna być najmniejsza, a taki warunek spełnia właśnie zwykła średnia.

Funkcji logistycznej używa się m.in. przy budowie logistycznego modelu wzrostu dywidendy wypłacanej przez spółkę akcyjną. Metodę taką przedstawił J. B. Williams w pracy The Theory of Investment Value, wydanej w roku 1956. Założeniem Williamsa było przeświadczenie, że nawet wysokiej klasy przedsiębiorstwo nie jest w stanie zwiększać co roku dywidendy bez końca. Stąd też należy przyjąć, że z początku (np. przez pierwszych kilka lat wypłacania dywidendy) tempo wzrostu wypłaty jest wysokie (to względne pojęcie – ale istotne jest to, że chodzi o jakąś stałą, dodatnią wartość), a następnie zaczyna spadać – teoretycznie aż do zera.

Mówimy tu o szybkości wzrostu dywidendy, a nie o samej kwocie tejże. Otóż zmiana kwoty układa się właśnie według funkcji logistycznej, opisanej wyżej, o ile tylko przyjmiemy założenia Williamsa, z których wynikają następujące wzory:

Przyjmujemy tu, że DIV to wysokość dywidendy, n to liczba owych początkowych lat, gdy tempo wzrostu jest stałe, zaś g to właśnie to stałe tempo. W oparciu o te aksjomaty i obliczenia można wyprowadzić wzór na bieżącą cenę akcji, który wygląda tak:

W tym dość skomplikowanym (przynajmniej z perspektywy kogoś, kto chciałby dokonywać ręcznych rachunków) wzorze pojawia się wartość r. Otóż jest to wymagana stopa zwrotu, której oczekujemy od inwestycji w akcję. W szczególności, w uproszczonych rozważaniach teoretycznych, może ona być równa wartości g, co oczywiście znacznie uprości wzór.

Adam Witczak

Bibliografia:

Elementy matematyki dla studentów ekonomii i zarządzania. Wybrane zastosowania, praca zbiorowa, Wydawnictwo Akademii Ekonomicznej w Katowicach 2007.

K. Pera, R. Buła, D. Mitrenga, Modele inwestycyjne, C. H. Beck, Warszawa 2014.