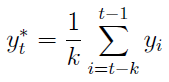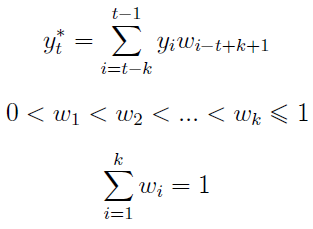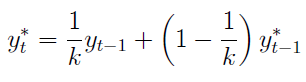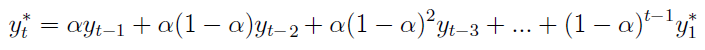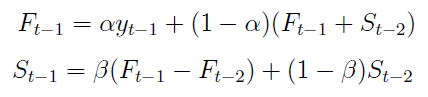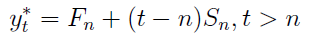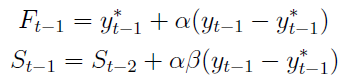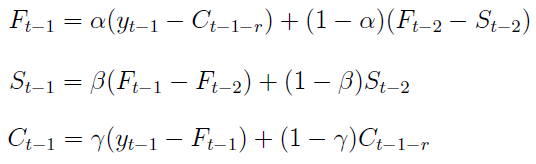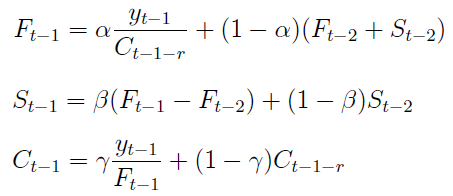Wygładzanie wykładnicze

Podstawą naszych rozważań będzie pojęcie szeregu czasowego. W ujęciu probabilistycznym można postrzegać taki szereg jako konkretną realizację procesu stochastycznego. Taki proces to z kolei funkcja losowa, ta zaś jest rodziną zmiennych losowych, indeksowaną parametrem t przebiegającym pewien zbiór T.

W rzeczywistości ów parametr najczęściej utożsamiamy z czasem, a zatem funkcja losowa opisuje wartości zmiennej w kolejnych chwilach. Wartości te przyjmowane są z pewnym prawdopodobieństwem. Te, które faktycznie uzyskaliśmy w danym okresie, tworzą szereg czasowy.

Więcej o takim podejściu pisaliśmy w odrębnym artykule na temat procesów stochastycznych. W gruncie rzeczy probabilistyka nie jest nam jednak dziś potrzebna. Szereg czasowy możemy traktować po prostu jako ciąg liczb, obrazujących zmianę danej wielkości w czasie. Tą wielkością może być np. kurs akcji, temperatura powietrza czy poziom bezrobocia.

To, co nas interesuje, to badanie trendów, prognozowanie i wygładzanie szeregów. W tym ostatnim przypadku chodzi o to, by zniwelować wpływ dużych, ale chwilowych i mało reprezentatywnych zmian; inaczej mówiąc, by w pewien sposób uśrednić otrzymane wartości.

Nim przejdziemy do meritum, poczynimy pewne zastrzeżenia techniczne. Otóż nasze opracowanie ogranicza się do podstawowych informacji i głównych wzorów. Pomijamy większość formalnych dowodów i przejść rachunkowych, nie wdajemy się też w rozważania poboczne - np. na temat szacowania błędu prognozy. Dla zachowania jednolitej notacji wszystkie formuły prezentujemy w ślad za pracą P. Dittmana z książki "Prognozowanie gospodarcze" (vide bibliografia).

*

Na rynkach finansowych, w tym np. w analizie technicznej kursu akcji, często stosuje się średnie ruchome - proste i wykładnicze. Przypomnijmy ideę średniej prostej:

Prognozowana wartość zmiennej Y na moment t to właśnie y_t^*. Jak widać, rzecz polega na tym, że bierzemy k ostatnich momentów (np. 10 poprzednich sesji giełdowych) i sumujemy wartości wówczas odnotowane (np. kursy zamknięcia). Ale uwaga: każdą wartość dzielimy przez k. Innymi słowy, za wartość prognozowaną (czy też wartość "na dziś") uważamy po prostu średnią arytmetyczną ostatnich k liczb.

Współczynnik k określa się mianem stałej wygładzania. Jeśli jest duży, to dane są mocno wygładzone, co objawi się łagodnym kształtem wykresu średniej. Przeciwnie, przy niskim k wykres ów będzie wchodzić w częstsze i większe wahania. Przy małym k średnia ruchoma będzie powoli reagować na zmiany poziomu zmiennej, przy dużym - reagować będzie szybko.

Analitycy techniczni często wykorzystują dwie średnie. Jedna jest krótkookresowa (dla 5, 10 czy 15 sesji), druga długookresowa (dla 30 czy 45 sesji, a można brać jeszcze większe wartości). Odpowiednie przecięcia średnich traktowane są nawet jako sygnały kupna lub sprzedaży akcji. Sygnał kupna jest generowany, gdy średnia krótkookresowa przecina od dołu niemalejącą średnią liczoną z dużej liczby okresów. Za sugestię sprzedaży uznaje się natomiast przecięcie z góry nierosnącej średniej z wielu sesji przez średnią krótkookresową.

Model podstawowy jest bardzo prosty, ale bazuje na założeniu, iż wszystkie brane pod uwagę kursy (wartości, ogólnie rzecz biorąc, bo nie mówimy tylko o akcjach) są jednakowo ważne. Tymczasem naturalne wydaje się założenie, że nowsze poziomy są istotniejsze; inaczej mówiąc - że przynoszą one bardziej aktualne wiadomości o zjawisku, które badamy.

Z tego powodu konstruuje się nieco bardziej złożony model, oparty o średnią ważoną. Wzór wygląda tak:

Tym razem mamy sumę wartości z k okresów, przy czym każda z nich przemnożona została przez wagę w_i-t+k+1. Rozbieżność indeksów przy wartości i wadze może w pierwszej chwili widzieć, ale chodzi o to, by przy najstarszych kursach używać najmniejszych wag, a przy najnowszych - wag największych. Na przykład dla y_t-1 będziemy mieć wagę o numerze k, czyli faktycznie największą, jeśli spojrzymy na drugą linijkę. Oczywiście wszystkie wagi winny się sumować do 1.

*

Teraz wejdziemy w clou zagadnienia, tj. w wygładzanie wykładnicze. Podstawowy wzór jest rekurencyjny:

Jak widać, do wyliczenia wartości prognozowanej na moment t, potrzebujemy prognozy z momentu t-1, ważonej współczynnikiem (1 - 1/k). Osoby zainteresowane analizą techniczną zapewne wiedzą, o co chodzi: po lewej stronie mamy wartość EMA (średniej ruchomej wykładniczej) dla dzisiejszej sesji, po prawej korzystamy z EMA obliczonej dla sesji wczorajszej.

Oczywiście od czegoś trzeba zacząć. EMA możemy liczyć dla ostatnich 5, 10, 15 czy np. 45 momentów, ale dopuszcza się również branie za każdym razem wszystkich dostępnych danych. W przypadku kursu akcji oznaczałoby to, że pewne (niewielkie, ale jednak) znaczenie ma nawet cena z pierwszej sesji, choćby debiut giełdowy spółki nastąpił 10 czy 20 lat temu.

Jeśli 1/k oznaczymy przez α, to dzięki prostym przekształceniom możemy wygenerować następujący wzór:

Jak widać, we wzorze mamy niemal wyłącznie autentyczne wartości, dopiero w ostatnim składniku sumy pojawia się 'igrek z gwiazdką' dla momentu nr 1. Wspomnieliśmy jednak wyżej, że za tę wartość możemy przyjąć pierwszą z dostępnych obserwacji; albo wartość sprzed k momentów; dopuszcza się również średnią arytmetyczną kilku pierwszych wartości rzeczywistych.

Zauważmy, że wagi α, α(1-α), α(1-α)² itd. - są wykładniczo malejące. Teraz widzimy, dlaczego mówi się o wygładzaniu wykładniczym.

Parametr α w zasadzie nie musi być postaci 1/k (gdzie k to liczba rozważanych momentów). Przeciwnie, często to po prostu jakaś liczba z przedziału [0,1], którą wyznacza się eksperymentalnie. Kryterium to możliwie mały średni błąd prognoz wygasłych.

*

Kolejne podejście to tzw. model liniowy Holta. Pasuje on do szeregów, w których można rozpoznać zarówno trend, jak i pewne wahania przypadkowe. Na początek rozważa się dwa równania:

Są to dwie części ostatecznej formuły. Pierwsza część przybliża poziom samej zmiennej; druga przybliża jej przyrost. Parametry α i β wyznacza się eksperymentalnie, powinny należeć do zakresu [0,1]. Ostateczna wartość prognozowana wygląda tak:

W zasadzie za n rozsądnie jest przyjąć po prostu t-1. Skąd mamy wziąć wartości F₁ i S₁, które są potrzebne, bo model jest rekurencyjny? Często za F₁ przyjmuje się po prostu pierwszą wartość zmiennej prognozowanej (pierwszą wartość w szeregu), a za S₁ - różnicę y₂ - y₁. Jeśli natomiast mamy już oszacowaną liniową funkcję trendu (na podstawie wstępnej próbki), to możemy za F₁ przyjąć jej wyraz wolny, a za S₁ - współczynnik kierunkowy.

Równania na F_t-1 i S_t-1 można przedstawić również w taki sposób (dzięki przekształceniom matematycznym):

*

Trzecia rzecz to model Wintersa. Ten stosuje się, gdy mamy trend, komponent wahań przypadkowych, a do tego jeszcze wahania sezonowe według pewnej regularności.

Model ten może być konstruowany przy pomocy równań addytywnych lub multiplikatywnych. Pierwsze wyglądają tak:

Drugie prezentują się następująco:

F_t-1 pojmuje się jako wygładzoną wartość zmiennej prognozowanej w momencie t-1 (po wyeliminowaniu wahań sezonowych). S_t-1 to przyrost trendu w chwili t-1, zaś C_t-1 to ocena wskaźnika sezonowości. Przez α, β, γ rozumiemy parametry z przedziału [0, 1], zaś r to liczba faz cyklu.

P. Dittmann proponuje, by za F₁ przyjąć pierwszą wartość rzeczywistą zmiennej prognozowanej, tj. y₁. Za S₁ możemy uznać po prostu y₂ - y₁. Za C₁, ..., C_r możemy uznać średnie różnic (dla modelu addytywnego) lub ilorazów (dla multiplikatywnego) wartości zmiennej i wygładzonych wartości trendu, przy założeniu, że przy każdej różnicy bierzemy tę samą fazę cyklu sezonowego. Na przykład dla C₁ rozważamy wspomniane wyżej różnice dla pierwszych faz wszystkich sezonów.

Adam Witczak


BIBLIOGRAFIA:

P. Dittmann, "Prognozowanie na podstawie szeregów czasowych", w: "Prognozowanie gospodarcze. Metody i zastosowanie", praca zbiorowa pod red. M. Cieślak, PWN 2001.

M. Etzkorn, "Oscylatory", Wig Press 1999

A. Ganczarek-Gamrot, "Analiza szeregów czasowych", Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2014

A. Snarska, "Statystyka, ekonometria, prognozowanie. Ćwiczenia z Excelem", Placet 2005.

J. J. Murphy, "Analiza techniczna rynków finansowych", WIG PRESS 1999