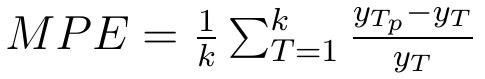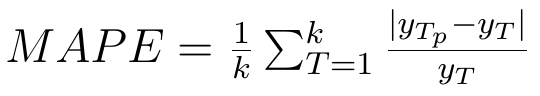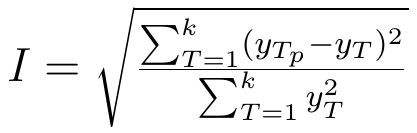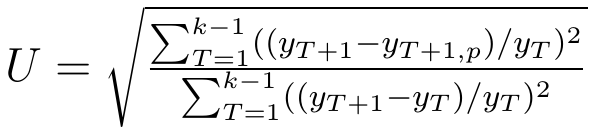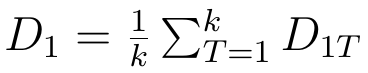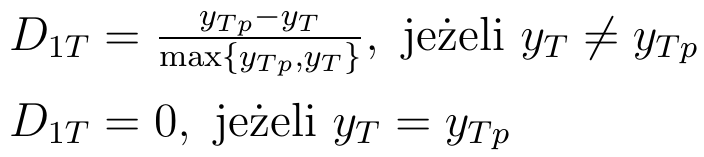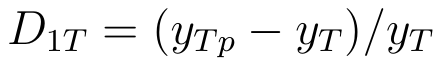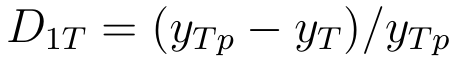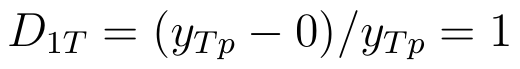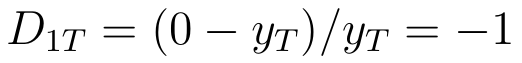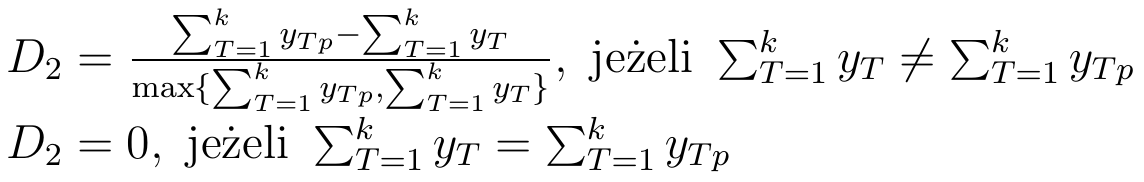Prognozowanie i błąd ex post

Prognozy ekonomiczne i finansowe (czyli przewidywania na temat przychodów, zysków, kursów walut, dynamiki PKB czy inflacji) rzadko kiedy sprawdzają się całkowicie dokładnie; ale przynajmniej czasami faktyczne rezultaty są do nich zbliżone. Trudno prowadzić biznes (albo zarządzać ministerstwem czy bankiem centralnym) bez jakichś założeń co do przyszłości.

Będziemy mówić o prognozach dotyczących przychodów ze sprzedaży). Niekiedy takie przewidywania można robić "na oko". Dotyczy to na ogół prostych biznesów. Niekoniecznie oznacza to biznesy małe; raczej takie, których model działania jest nieskomplikowany: bo np. wpływ na ich sytuację mają tylko nieliczne czynniki, a funkcja przychodów z jakichś przyczyn przybrała już dobrych kilka lat temu prostą, zrozumiałą postać. Cóż, jeśli "gołym okiem" widać, że obroty co roku są o połowę większe; albo że od dziesięciu lat mieszczą się w pobliżu 10 mln zł, z maksymalnie 10-procentowymi odchyleniami po obu stronach; albo że z każdym rokiem maleją o ok. 1/10 - to sytuacja jest w miarę jasna i być może menedżerowie mogą zaoszczędzić na analitykach.

W praktyce jednak sprawy są bardziej skomplikowane. Obroty tygodniowe (tak samo roczne, półroczne czy kwartalne; ale trzeba jakiś okres ustalić) raz maleją, raz rosną, zdarzają się sytuacje nieoczekiwane, obraz jest złożony. Wówczas sięga się po metody matematyczne: i można prognozować np. przy pomocy funkcji liniowych, wykładniczych albo logistycznych (tudzież jeszcze innych).

Po kilku okresach wypada jednak ocenić i to, czy nasze prognozy się sprawdziły; albo raczej - w jakim stopniu się sprawdziły. Innymi słowy, trzeba zbadać ich błąd (i np. porównać go z błędem cechującym inne, alternatywne modele prognostyczne).

W dalszej części tego tekstu będziemy (skrótowo) referować przede wszystkim pracę M. Doszynia (por. bibliografia), w której zaprezentowano pewne znane i powszechnie używane formuły oceny efektywności prognoz, a także ciekawe (i dość proste) rozwiązanie autorskie. Zaznaczmy, że mowa jest o błędach ex post: a więc nie o teoretycznej dokładności statystyk prognostycznych, lecz o tym, jak faktycznie one wypadły.

Przyjmijmy następujące oznaczenia:

k - liczba prognoz (w domyśle: liczba tygodni, które były brane pod uwagę; mogą to oczywiście być też prognozy miesięczne czy roczne, acz z pewnych względów rozważania dotyczą raczej krótszych okresów),

y_Tp - wartość prognozy w tygodniu T (czyli przychody, jakie przewidywano na tydzień o numerze T),

y_T - faktyczne przychody w tygodniu T.

Oczywiście łatwo ocenić w każdym tygodniu, o ile (zł lub proc.) realne obroty różnią się od prognozowanych; ale jeśli mamy kilka tygodni, to trzeba jakoś tę różnicę uśrednić. Wbrew pozorom miernikiem nie musi być (choć może) średnia arytmetyczna z odchyleń. Stosowane są m.in. poniższe formuły:

1) Średni błąd procentowy (MPE):

2) Średni absolutny błąd procentowy (MAPE):

3) pierwszy współczynnik Theila:

4) drugi współczynnik Theila:

M. Doszyń zauważa istotny problem: te mierniki mogą być stosowane tylko wtedy, gdy w każdym okresie (tygodniu) sprzedaż jest dodatnia. Obrotów ujemnych oczywiście nie uwzględniamy, ale może się zdarzyć, że będą one w niektórych tygodniach zerowe. Innymi słowy, może być tak, że nie doszło do żadnych aktów sprzedaży produktów lub usług. Wtedy w mianownikach ułamków (w powyższych wzorach) będziemy mieć zera, czyli dzielenie będzie niewykonalne, a wzór bezużyteczny.

Autor referowanej pracy proponuje następujące rozwiązanie tego problemu: wykorzystanie tzw. średniego błędu cząstkowego. Wzór widzimy poniżej:

Błędy cząstkowe dla poszczególnych tygodni liczy się następująco:

Jak należy to rozumieć? Jeśli w danym tygodniu T przychody rzeczywiste były równe prognozowanym, to przyjmujemy, że D_1T też jest zerowy. Czyli nie ma błędu (a ściślej, wynosi on zero). Jeżeli były różne, to sprawdzamy różnicę pomiędzy wynikiem teoretycznym a wynikiem faktycznym, a potem dzielimy ją przez większy z tych wyników. Jeśli prognoza jest niższa od faktycznej kwoty, to błąd przyjmuje formę:

Jeśli prognoza była wyższa od faktycznej sumy, to mamy:

Zauważmy, że przypadek, w którym prognoza i realna kwota są równe, czyli przypadek D_1T = 0, "załatwia" nam również kłopotliwą sytuację, w której y_Tp = y_T = 0.

A co wtedy, gdy tylko jedna z wartości jest zerowa? Jeśli przychody faktyczne są równe 0, a prognozowane większe od zera, to:

Jeśli natomiast przychody faktyczne są większe od zera, a prognozowane równe 0:

Warto też odnotować, że błąd D_1T ma charakter znormalizowany, mianowicie należy do przedziału [-1, 1].

Autor prezentuje także wariant wzoru, w którym pracuje się z sumami prognoz dla k tygodni:

Czytamy też o pewnym mankamencie tej metody (to znaczy obu wariantów wzoru). Otóż: "Należy mieć świadomość, iż w liczniku nie występuje wartość bezwzględna odchyleń prognoz od wartości empirycznych, przez co błędy prognoz mogą się znosić. Między innymi dlatego należy analizować rozkłady analizowanego błędu, a nie np. tylko wartości średnie".

Dowiadujemy się również, że "Jeżeli celem prowadzonej polityki jest jak najlepsze zaspokajanie popytu, to należy szczególną uwagę zwracać na produkty, dla których omawiany błąd jest ujemny (prognozy są zaniżone)", a "Jeżeli celem jest zmniejszanie stanu zapasów, trzeba dużą wagę przywiązywać do produktów, dla których błąd jest dodatni (prognozy są zawyżone)".

W pracy zamieszczono także empiryczną ilustrację skuteczności metody (acz pominięto kod programu, który jest jej komputerową implementacją).

Adam Witczak

BIBLIOGRAFIA:

P. Dittmann, E. Szabela-Pasierbińska, I. Dittmann, A. Szpulak, "Prognozowanie w zarządzaniu sprzedażą i finansami przedsiębiorstwa", Wolters Kluwer Polska 2011.

M. Doszyń, "Sposoby badania trafności systemu prognoz sprzedaży w przedsiębiorstwie", w: "Studia Ekonomiczne. Zeszyty Naukowe Uniwersytetu Ekonomicznego w Katowicach", nr 241 (2015).

A. Ganczarek-Gamrot, "Analiza szeregów czasowych", Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2014.