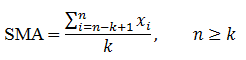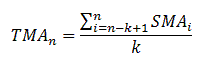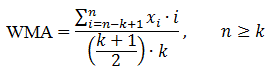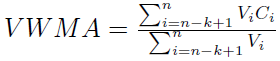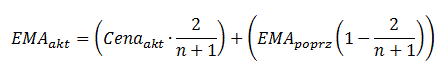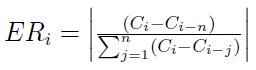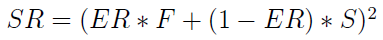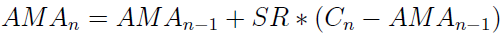Średnie ruchome na wykresach

Tematem naszych dzisiejszych rozważań będą średnie kroczące. Należą one do podstawowych, najpopularniejszych i zarazem najprostszych (tak w użytkowaniu, jak i w konstrukcji) narzędzi analizy technicznej wykresów giełdowych.

Jak wiadomo, wskaźniki techniczne (z których wiele opiera się zresztą na średnich) nie dokonują żadnego cudu, w szczególności nie dają żadnej informacji, która nie byłaby uprzednio ukryta w wykresie cen. Rzecz jednak w słówku "ukryta". Otóż wskaźniki, poprzez wygładzanie danych, eliminowanie szumu i skrajnych wartości - pozwalają zobrazować to, czego ludzkie oko samo nie wychwyci. Ich interpretacja opiera się oczywiście na pewnych założeniach, zgodnych ze zdrowym rozsądkiem - np. uważa się, że uśrednione wyniki lepiej wyrażają generalny kierunek zmian niż chwilowe, niepokojące deformacje.

Przypomnimy zatem, jakich średnich używa się najczęściej. Podamy wzory, które później zilustrujemy wykresami - zaczerpniętymi albo z godnego polecenia polskiego programu Power Trader (dane z GPW), albo z programu Marketscope przy platformie FXCM (dane z rynku forex). Przed prezentacją wykresów powiemy kilka słów o tym, co jest najistotniejsze - tj. o wyszukiwaniu sygnałów dawanych przez opisywane narzędzia. Interpretacja jest zresztą bardzo podobna w każdym przypadku, jakkolwiek same średnie różnią się od siebie sposobami obliczania i prezentacją graficzną.

Oto krótki katalog formuł:

Prosta średnia ruchoma (Simple Moving Average – SMA)

Jest to po prostu średnia arytmetyczna kursów z k ostatnich okresów (sesji). Średnia ta „przesuwa się” w czasie, tzn. na każdym kroku z obliczeń wyłącza się najstarszy odczyt, dzięki czemu liczba branych pod uwagę odczytów pozostaje stała. Fakt ten obrazowany jest dość klarownie w poniższym wzorze:

Przyjmujemy oznaczenia:

x_i – kurs (wartość) w i-tym kroku (podczas i-tej sesji); zazwyczaj bierzemy pod uwagę kurs zamknięcia, aczkolwiek można sobie wyobrazić korzystanie z dowolnego innego (np. ze średniego kursu z dnia)

k – liczba okresów, z których wyliczamy średnią (np. liczba dni, ale mogą to być godziny czy tygodnie)

Trójstronna średnia gładzona (Triangular Moving Average – TMA)

Jest to po prostu ponownie uśredniona (w zwykły sposób) średnia SMA. W większym stopniu wpływają na nią dane ze środkowej części badanego interwału i jest bardziej wygładzona w stosunku do wykresu SMA czy kursu.

Ważona średnia ruchoma (Weighted Moving Average – WMA)

Przeszłości nie można całkowicie ignorować, ale jednak można podejrzewać, że starsze ceny są mniej ważne dla inwestorów, zaś nowsze notowania mogą mieć realny wpływ na przyszłość. Taka intuicja prowadzi do idei ważonej średniej ruchomej. Kolejnym wartościom kursu przypisuje się określone wagi, oddające istotność danej sesji. Wagi te mogą być przypisywane po prostu na zasadzie postępu arytmetycznego z krokiem równym 1 – wówczas najstarsza cena ma wagę 1, kolejna 2, najnowsza natomiast k. Otrzymujemy wtedy następującą formułę:

Średnia krocząca ważona wolumenem (Volumen Weighted Moving Average - VWMA)

Istnieje wiele wskaźników analizy technicznej, które w jakiś sposób uwzględniają wolumen. W swoim czasie poświęciliśmy temu nawet odrębny artykuł, w którym omówiliśmy On Balance Volume (OBV) oraz narzędzia proponowane przez Richarda W. Armsa.

Jakie jest znaczenie wolumenu? Naturalne wydaje się przeświadczenie, że jeśli rośnie wraz z określonym kierunkiem cen, to fakt ten stanowi wyraz autentycznego poparcia graczy dla takiego właśnie kierunku. Jeśli natomiast zmiany następują przy małym wolumenie, przy handlu małą liczbą akcji - to ruchy cen stają się mało wiarygodnie. Ma sens pogląd, że jeśli ceny jeszcze rosną, ale wolumen już maleje – to znaczy, że część graczy wycofuje się z rynku i za chwilę zabraknie sił do dalszego prowadzenia hossy.

Wzór na średnią ważoną wolumenem wygląda tak (przyjmujemy, że V_i to wolumen z danej sesji, odpowiadający cenie zamknięcia C_i):

Wykładnicza średnia ruchoma (Exponential Moving Average – EMA)

Wagi mogą być dobierane także na inne sposoby. Wagi liniowe sprawdzają się głównie przy instrumentach, których ceny zmieniają się powoli i bez gwałtownych ruchów. W innych przypadkach sytuacja się komplikuje. Dlatego bardzo często wykorzystuje się wykładniczą średnią ruchomą. Z matematycznego punktu widzenia można ją opisać kilkoma wzorami (dokładnymi i przybliżonymi). Najczęściej stosuje się podejście rekurencyjne:

Oznaczenia są następujące:

EMA_akt – wartość średniej w danym momencie, którą chcemy obliczyć

Cena_akt – aktualna cena (może to być np. średnia cena z dnia lub cena zamknięcia)

EMA_poprz – poprzednia wartość EMA.

EMA liczona bywa dla rozmaitych okresów, np. dla 5, 10 czy 15 okresów. W teorii można sobie oczywiście wyobrazić  obliczanie jej nawet dla wszystkich danych, od samego początku notowań (powyższy wzór na pozór sugeruje nawet takie rozwiązanie). Wtedy najstarsze kursy byłyby rzecz jasna bardzo mało istotne, ale jednak miałyby swoje znaczenie - choć sama średnia, pomijając spółki o małym stażu, przyjęłaby bardzo wygładzoną postać. Nawiasem mówiąc, niekiedy analitycy stosują średnie (EMA, SMA czy WMA) liczone nawet dla 150 sesji, co pozwala na długoterminowych wykresach wychwycić najbardziej ogólne tendencje.

Adaptacyjna średnia ruchoma Kaufmanna (Kaufman Adaptive Moving Average - AMA / KAMA)

Ten wynalazek jest zbliżony swą formułą do średniej EMA. Zauważmy, że w EMA mamy współczynnik propocji - jest nim ułamek 2 / (n+1). W AMA występuje coś podobnego, ale tym razem współczynnik codziennie się zmienia. Innymi słowy, nie jest tak, że średnia na dany dzień zależy zawsze w takim samym stopniu od średniej wczorajszej i aktualnej ceny. To, która wielkość jest ważniejsza, zmienia się w czasie.

Procedura zaczyna się od wyliczenia tzw. wskaźnika ER (Efficiency Ratio) - na przykład w i-tym dniu, rozpatrując jako przeszłość n = 10 okresów. Jego wzór wygląda tak:

Wskaźnik ten mierzy obecność trendu na rynku - jeśli wartość (która obejmuje zakres od 0 do 1) jest bliska 1, to znaczy, że występuje jakiś trend (spadkowy lub wzrostowy).

Następny krok to wyliczenie wielkości F i S, przy czym na ogół F = 2/3, zaś S = 2/31. Stanowi to nawiązanie do średnich ruchomych - 2-dniowej i 30-dniowej. Później wyliczamy współczynnik proporcji SR:

I wreszcie przychodzi czas na finalny wzór AMA:

W jaki sposób interpretujemy ruch średnich? Pierwsza, najprostsza metoda to użycie na wykresie jednej średniej - i patrzenie na to, jak ma się do niej wykres cen. W zasadzie moglibyśmy powiedzieć, że jeśli średnia rośnie lub spada, to już jest to oznaka tego, że kursy idą w takim właśnie kierunku. W praktyce stosuje się jednak subtelniejsze interpretacje, do pewnego stopnia eliminujące zwodnicze sygnały.

Otóż jeśli wykres kursu (a najlepiej - cena zamknięcia) przecina od góry nierosnącą linię średniej kroczącej, to ruch taki zwiastuje dalszy spadek cen, a zatem sugeruje włączenie się w sprzedaż. Kiedy wykres kursu przecina od dołu niemalejącą linię średniej kroczącej, wówczas powinniśmy kupować, bo ceny prawdopodobnie będą dalej rosły.

Bardzo wygodne jest też posługiwanie się dwiema średnimi - krótkookresową (wyliczoną np. dla 5, 10 czy 15 okresów) i długookresową (np. dla 30 czy nawet 45 sesji). Sygnał kupna następuje, gdy średnia krótkookresowa przecina od dołu niemalejącą średnią liczoną z dużej liczby okresów. Odwrotnie: sygnałem sprzedaży jest przecięcie z góry nierosnącej średniej z wielu sesji przez średnią krótkookresową.

W pewnym sensie szybka średnia popędza powolną, wyprzedza ją, niejako pieczętując kierunek cen. Podobnie zachowują się same ceny w pierwszej interpretacji - tak jakby mówiły: "średnia ma rację, zatem idźmy na całość". To oczywiście cokolwiek artystyczna wizja, którą czytelnik winien nam wybaczyć.

Analitycy oczekują niekiedy potwierdzeń sygnałów i próbują to do pewnego stopnia formalizować. Na przykład sprawdza się, czy cena zamknięcia przebiła średnią o pewną określoną wartość (kwotową lub procentową). Można też odczekać kilka sesji, by sprawdzić, czy sygnał faktycznie obrazował trwałe zjawisko (ale wtedy nie załapiemy się już na początkowe dni wzrostów).

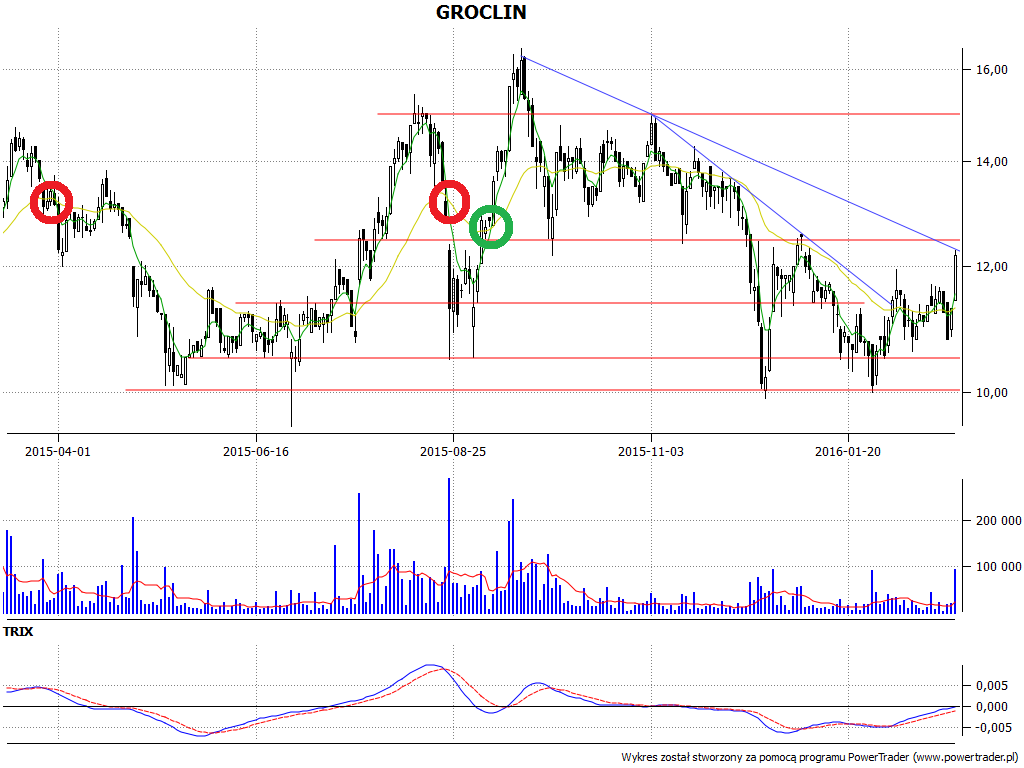
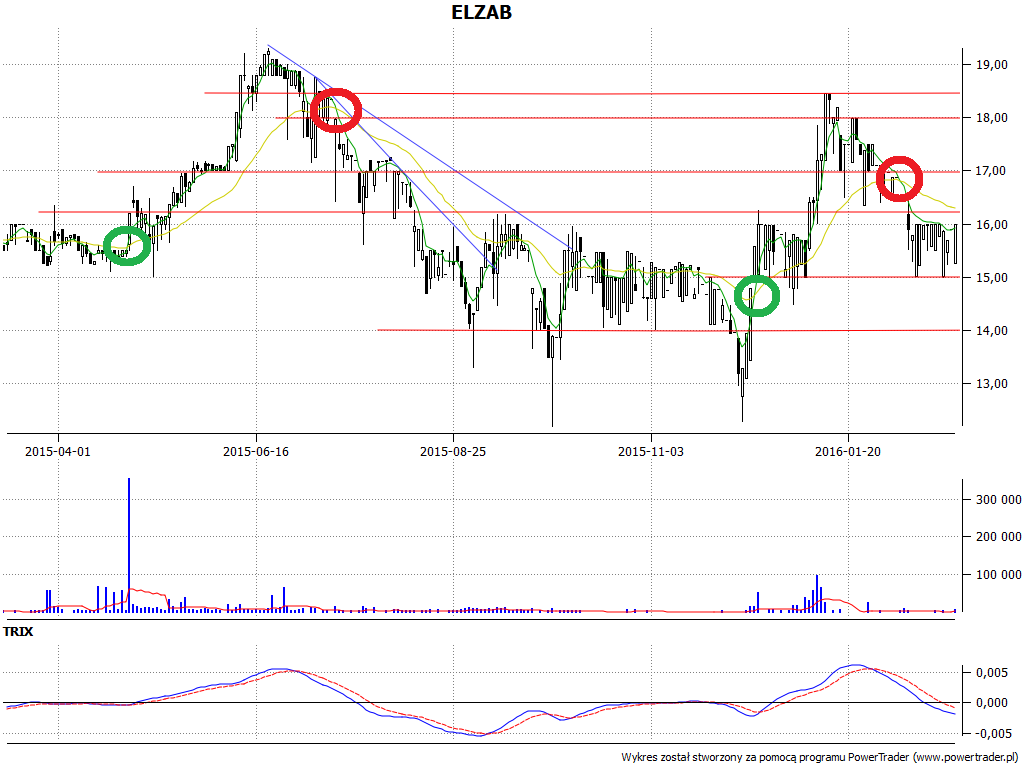
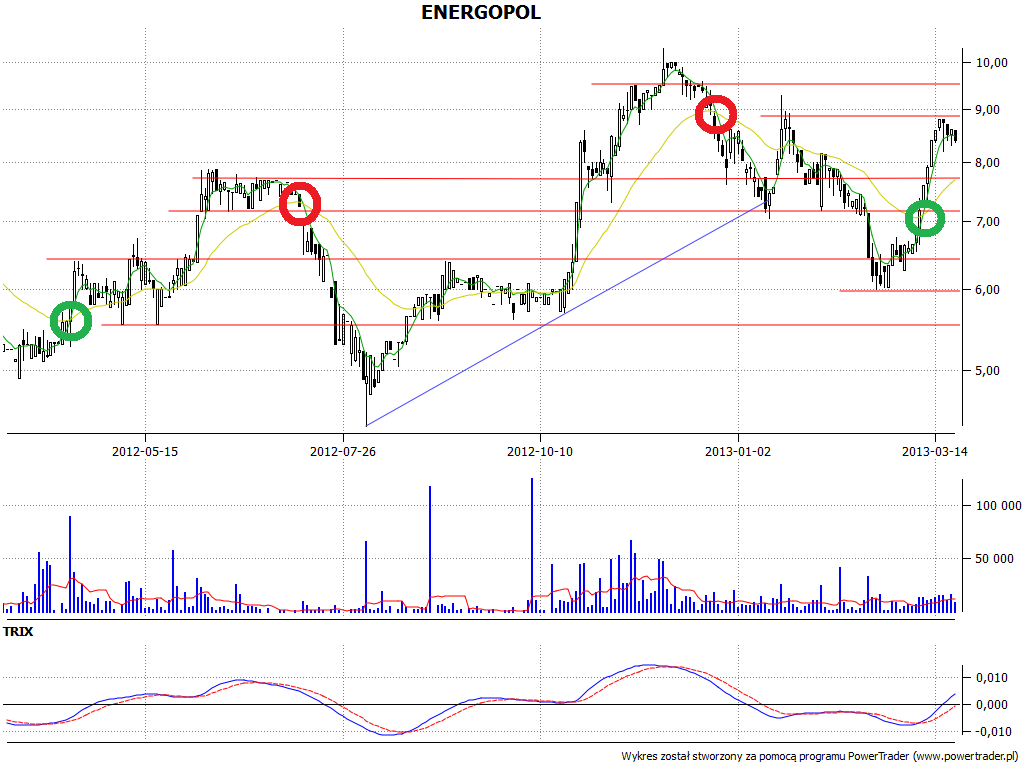
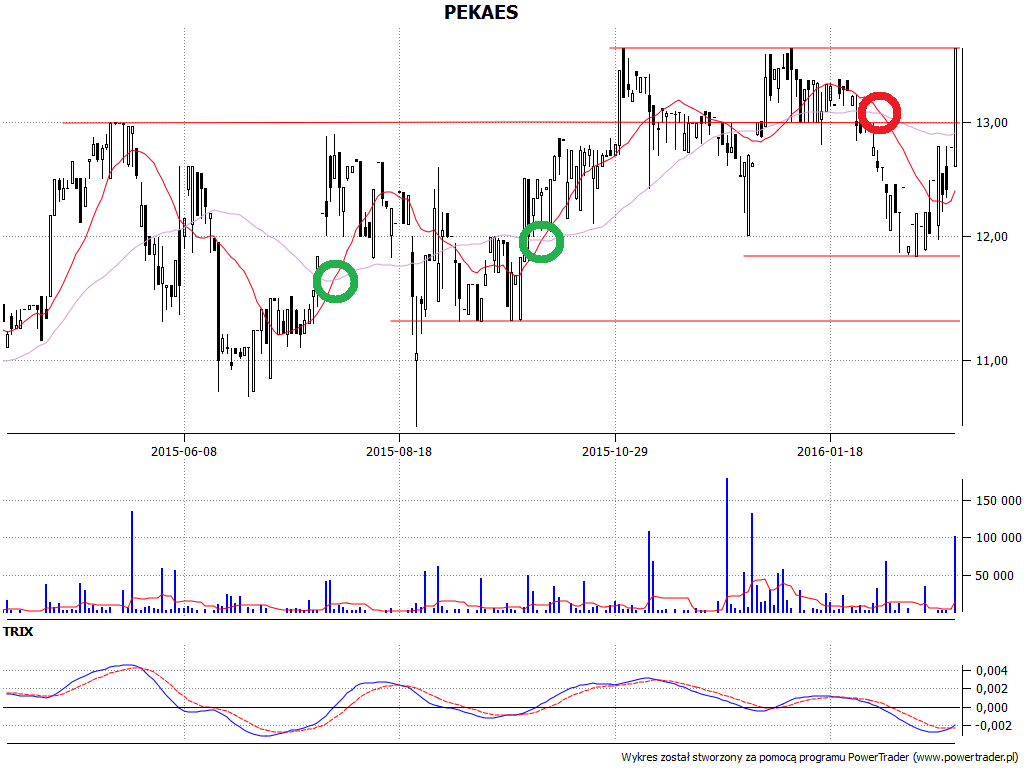
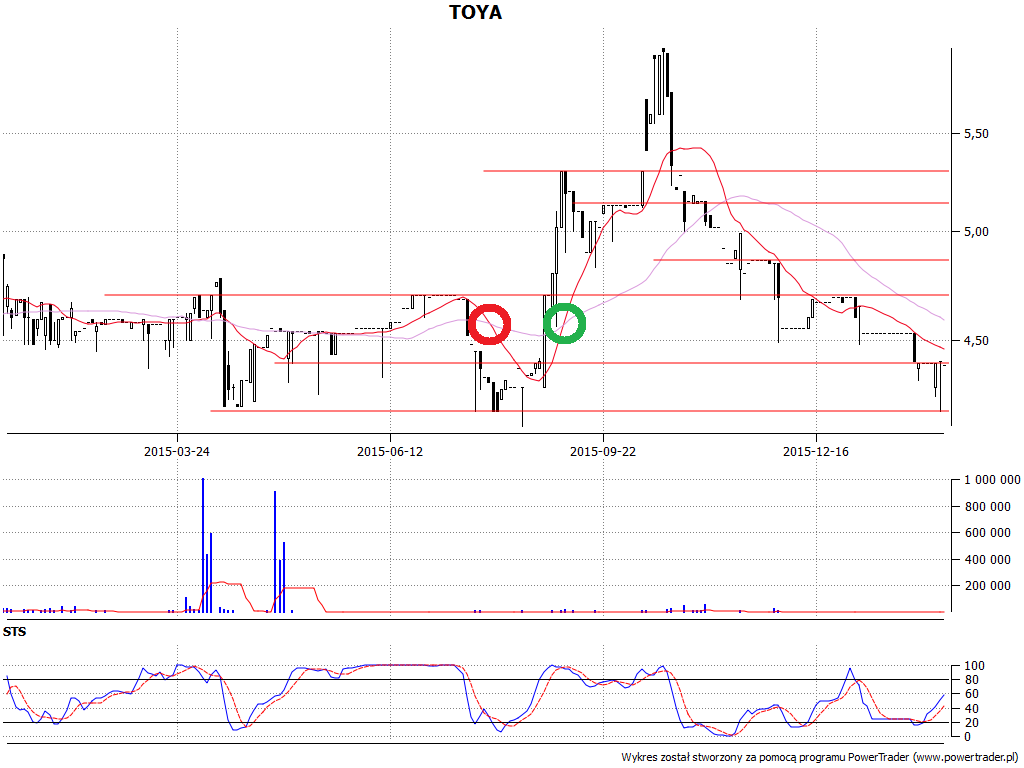
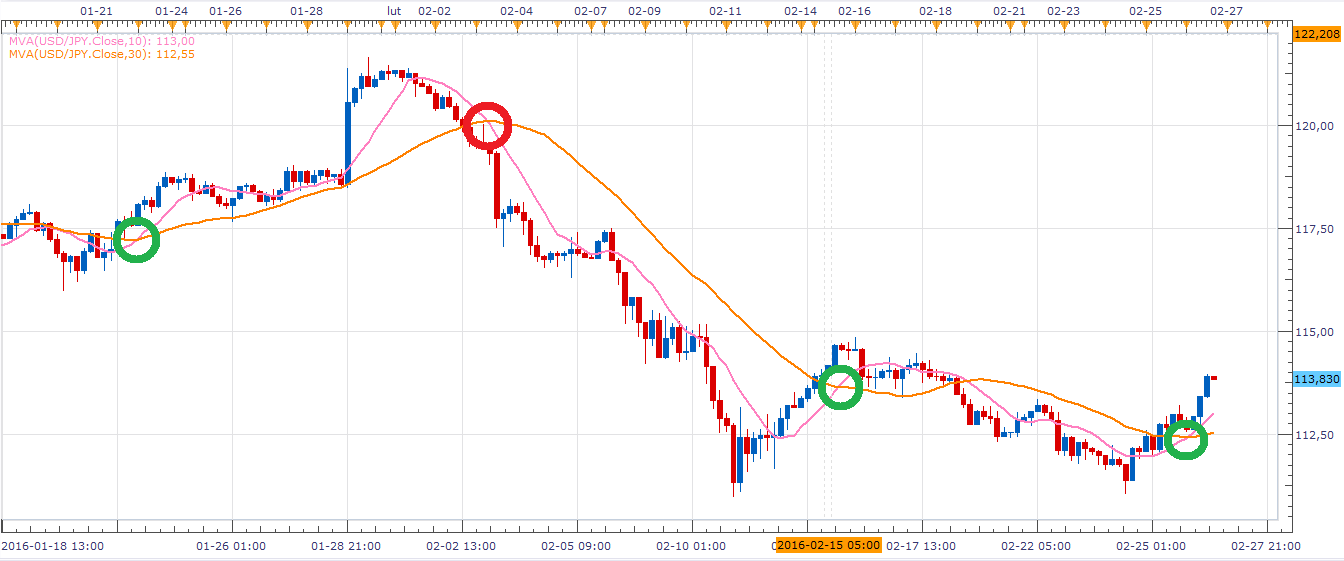
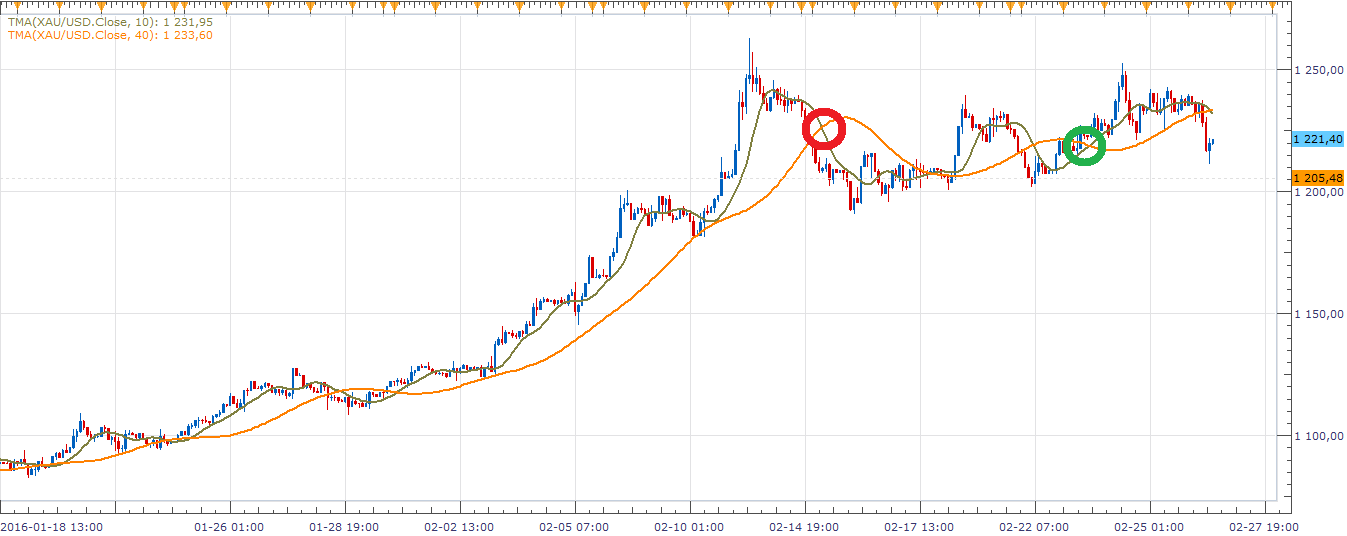
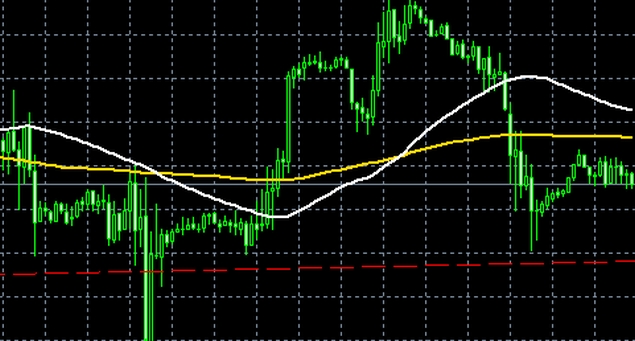
Jak to wygląda w praktyce? Spójrzmy najpierw na przypadek EMA. Mamy cztery wykresy, na każdym wykorzystano EMA dwukrotnie - wyliczoną dla krótkiego i długiego okresu. Wykresy tych średnich nałożone są na wykres cen, zazwyczaj tak się właśnie robi. Czerwone kółka to sygnały sprzedaży, a zielone sugerują kupno walorów i dalszy wzrost cen.

Łatwo zauważyć, że w zaznaczonych miejscach nasza metodologia się sprawdziła (no cóż, w analizie technicznej na ogół wszystko wygląda bardzo dobrze, ale po fakcie - moglibyśmy dodać zgryźliwie). Naturalnie są też momeny, w których średnie nie zadziałały wystarczająco szybko i sprawnie - np. na wykresie Energopolu po 18 maja 2012 mamy parcie cen w górę, aż do 7,87 zł, ale średnie EMA najpierw ocierają się o ciebie, co trudno nazwać precyzyjnym sygnałem, a potem rozbiegają.

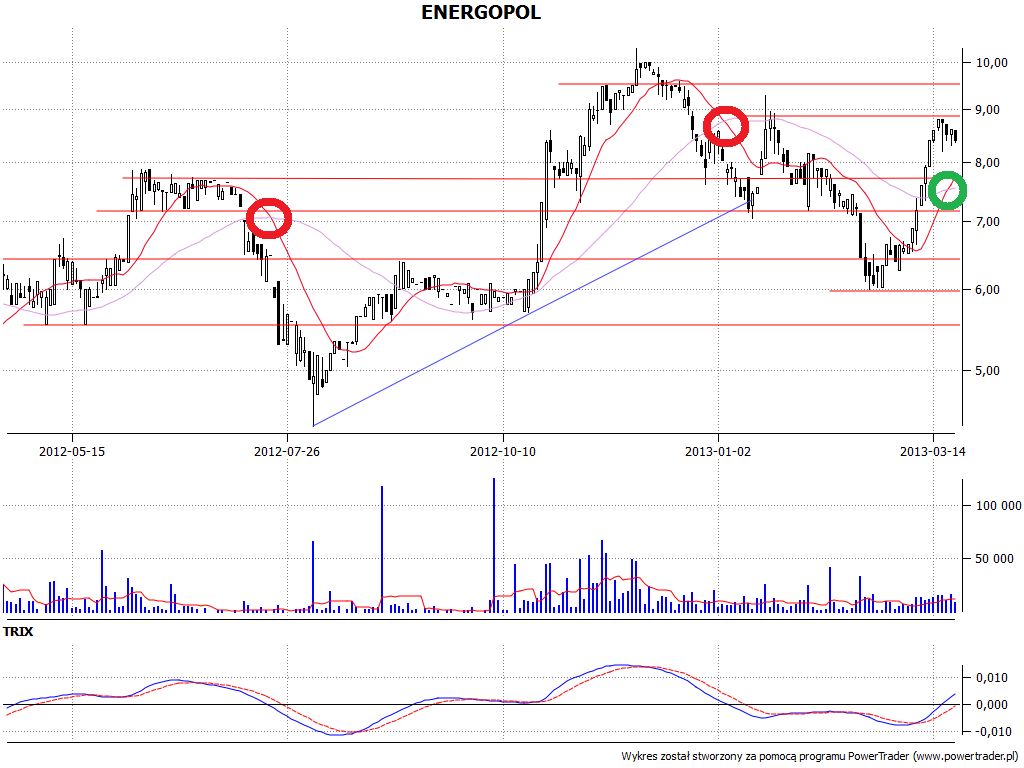
Porównajmy te obrazy ze średnią SMA:

Rzuca się w oczy to, że często reaguje ona z opóźnieniem na wykresach z GPW - ale to akurat nasza sprawka, bo EMA liczona była dla 5 i 30 dni, zaś SMA dla 15 i 45 dni. Chcieliśmy bowiem zobrazować nie tylko różnicę między EMA i SMA, ale też kwestię tego, jakie okresy rozpatrywać. Jeśli są to zbyt krótkie odcinki czasu, to średnie niemal pokrywają się z wykresem, co nie daje nowych informacji. Jeśli są zbyt długie - to sygnały pojawiają się rzadko i mogą być opóźnione.

Swoją drogą, widzimy np., że drugi sygnał sprzedaży na wykresie Energopolu - ten z samego progu roku 2013 - jest trochę "nieortodoksyjny". Oto bowiem powolna średnia nie jest niemalejąca - jeszcze rośnie, gdy linia szybka ją przecina. Analityk sztywno przywiązany do książkowych reguł mógłby ten sygnał pominąć. Faktem jest jednak, że niektórzy autorzy (np. John J. Murphy w swej słynnej "Analizie technicznej rynków terminowych") za wystarczający sygnał uważają po prostu sam fakt przecięcia.

Niżej mamy TMA i WMA:

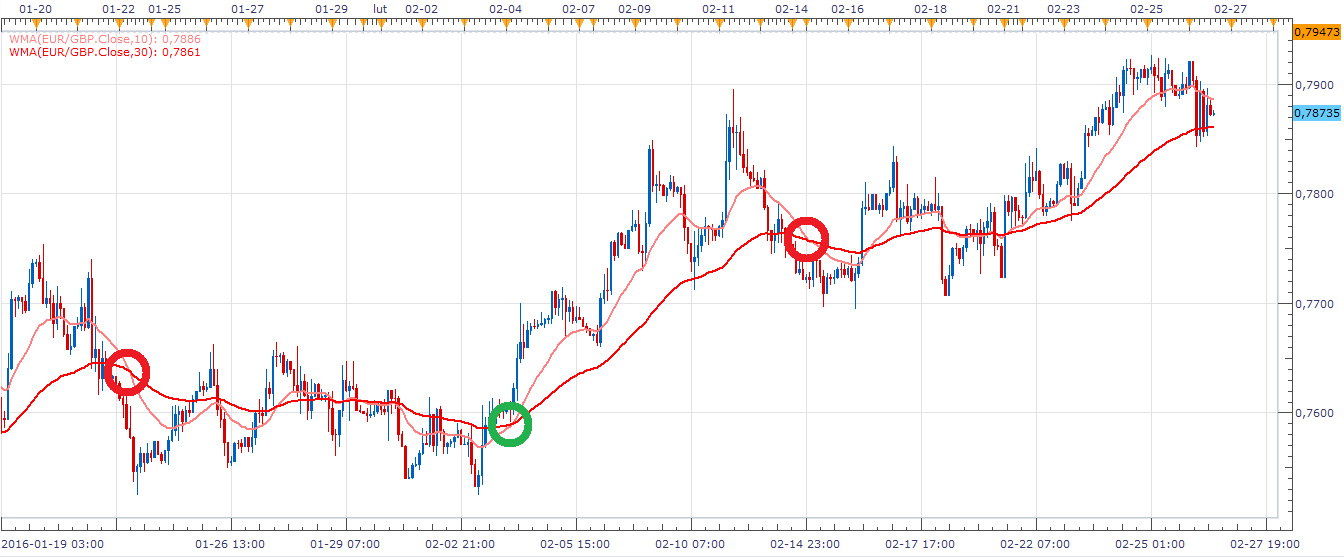
Jak widać, wszystko wygląda podobnie jak na poprzednich wykresach. Zauważmy jednak, że np. na wykresie EUR/GBP z WMA 10-dniową i 30-dniową dwa sygnały pro-sprzedażowe, które zaznaczyliśmy, wystąpiły długo po rozpoczęciu się spadków. Mogłyby nas one jedynie utwierdzić w tym, jaka jest tendencja, ale gdy spadki się zaczynały, to o przecięciach nie było jeszcze mowy. Naturalnie nie twierdzimy, że to jakaś specyficzna zła cecha WMA - po prostu to cecha średnich. Nie pozostaje nic innego, jak stosować równolegle kilka metod i wskaźników. Zresztą w obu wypadkach, o których mówimy, można było przed przecięciem zauważyć przebijanie średniej (szybkiej) przez ceny.

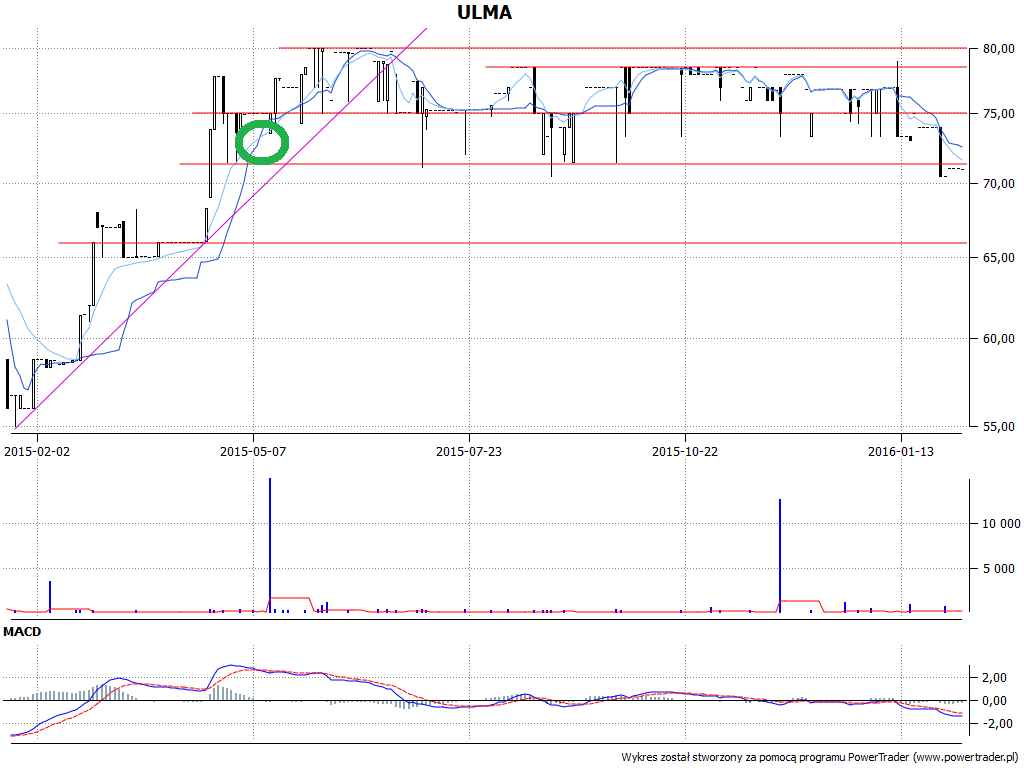
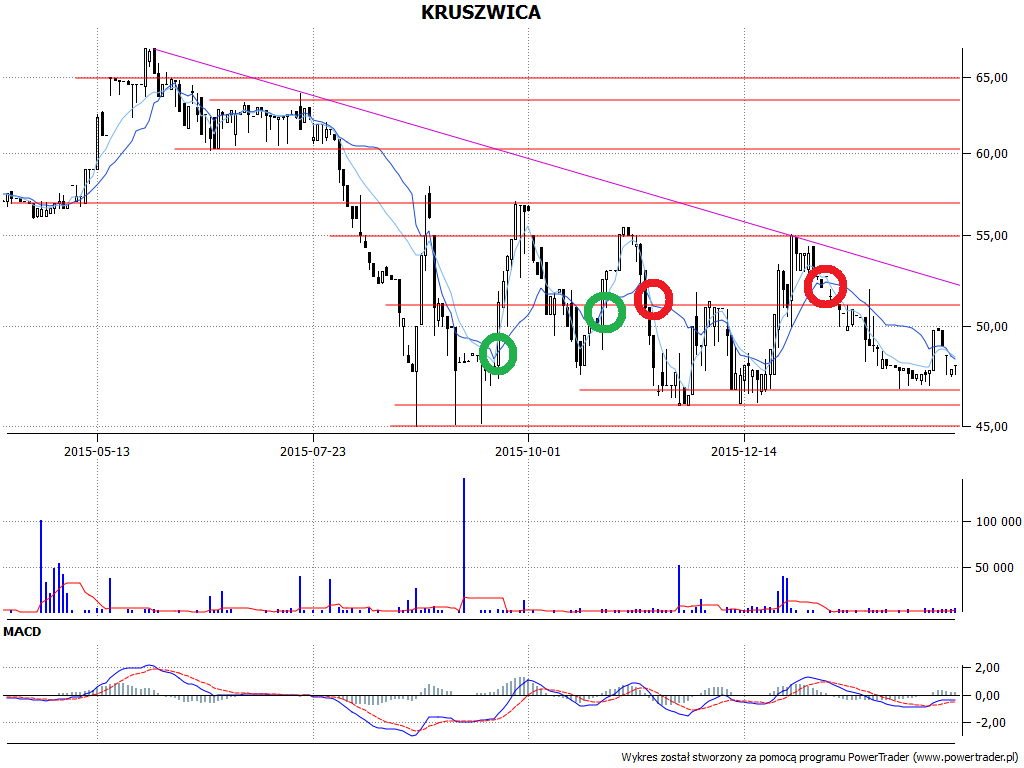
A teraz AMA:

Także i tu metoda przecięć z pewnością nie wyłapuje wszystkich momentów rozpoczęcia wzrostów, niemniej zaznaczyliśmy pewne oczywiste i następnie zrealizowane sygnały.

W tym krótkim opracowaniu nie omówiliśmy oczywiście ani wszystkich niuansów, ani wszystkich metod korzystania ze średnich. W szczególności nie rozważamy wskaźników budowanych przy pomocy średnich ruchomych. Powiemy tylko, że przykładami takich narzędzi są popularne funkcje MACD, POS czy TRIX.

Adam Witczak

BIBLIOGRAFIA:

M. Czekała, "Analiza fundamentalna i techniczna", Wydawnictwo Akademii Ekonomicznej im. Oskara Langego we Wrocławiu 1997

J. J. Murphy, "Analiza techniczna rynków finansowych", WIG PRESS 1999

M. Krzywda, "GPW IV. Analiza techniczna w praktyce", Złote Myśli 2010.