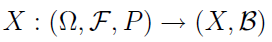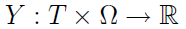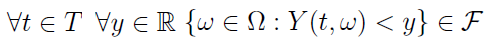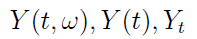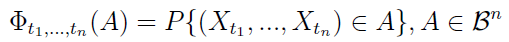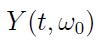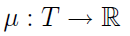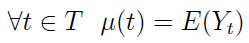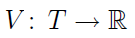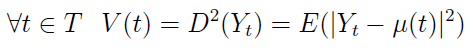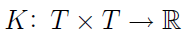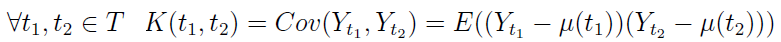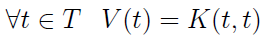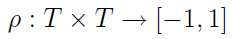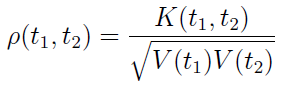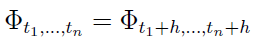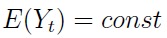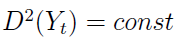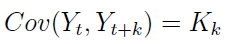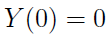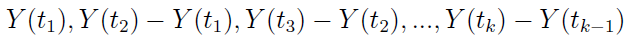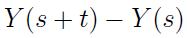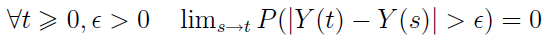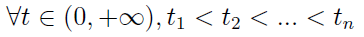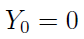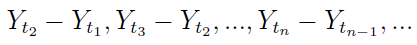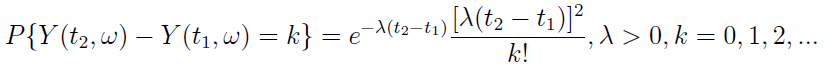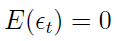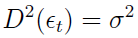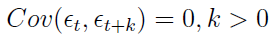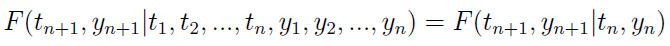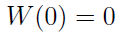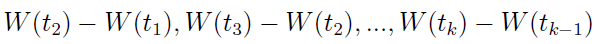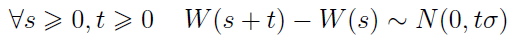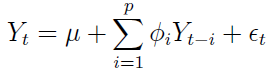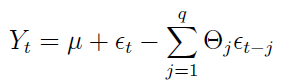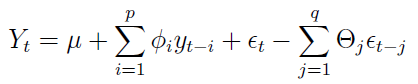Procesy stochastyczne

Procesy stochastyczne i szeregi czasowe są narzędziami powszechnie wykorzystywanymi w mikro- i makroekonomii, analizie finansowej, ekonometrii czy analizie technicznej wykresów giełdowych.

Stwierdzenie powyższe jest oczywiście truizmem, a przynajmniej powinno być tak traktowane. Teoria procesów stochastycznych banalna jednak nie jest - zaś to, co za chwilę zobaczymy i tak będzie co najwyżej wstępem do preludium.

Absolutnie podstawowym pojęciem musi być przestrzeń probabilistyczna. To trójka uporządkowana (Ω, F, P). Przez Ω rozumiemy zbiór zdarzeń elementarnych. F to rodzina wszystkich podzbiorów zbioru Ω, mierzalnych względem P - zaś P to miara probabilistyczna.

W zasadzie powinniśmy tu zejść jeszcze stopień niżej i wyjaśnić, czym jest miara probabilistyczna, a nawet - czym jest miara w ogólności. A także, co to takiego σ-ciało podzbiorów (w istocie F jest właśnie σ-ciałem). Tak naprawdę zakładamy jednak, że czytelnik zna podstawy rachunku prawdopodobieństwa (bądź co bądź wykładane na każdej uczelni ekonomicznej) lub przynajmniej zachował pewne ogólne, intuicyjne rozumienie omawianych pojęć. Wie zatem np., że wartość P musi mieścić się pomiędzy 0 i 1 (jako że jest to prawdopodobieństwo).

Zmienna losowa to funkcja X, która zdarzeniom elementarnym przypisuje wartości z pewnej mierzalnej przestrzeni X z miarą B. W praktyce są to na ogół liczby rzeczywiste. Zajmowanie się liczbami rzeczywistymi jest po prostu wygodniejsze niż działanie "bezpośrednio" na zdarzeniach elementarnych.

Jeżeli rzucamy dwiema kostkami do gry i interesuje nas suma oczek, to zdarzeniami elementarnymi będą wszystkie możliwe sumy (a ściślej: sytuacje, np. układ "3 na pierwszej kostce, 2 na drugiej"). Tym sytuacjom możemy przypisać odpowiednie liczby. Suma oczek jest więc zmienną losową. Taką zmienną może być też np. kurs akcji (w każdym razie ma sens traktowanie go w ten sposób). To poniekąd tylko formalność: zdarzeniu "cena wynosi 5 zł" przypisujemy liczbę 5. Czyli "nic się nie dzieje". Ale już np. orzeł i reszka w monecie nie są "same z siebie" powiązane z liczbami, tak więc w tym przypadku musimy wykonać pewną "pracę" i np. ustalić, że orzeł będzie utożsamiany z liczbą 1, zaś reszka z liczbą 0.

Kolejna rzecz to funkcja losowa (jednowymiarowa). Jest to funkcja, która pobiera zarówno zdarzenie elementarne, jak i element pewnego zbioru T, po czym zwraca element przestrzeni mierzalnej, w praktyce - liczbę rzeczywistą:

Zakładamy przy tym następującą własność:

A zatem to po prostu rodzina zmiennych losowych indeksowana parametrem t przebiegającym pewien zbiór T. Naturalnie od razu narzuca się tu skojarzenie z czasem. I rzeczywiście: wyróżnia się przypadek, w którym T jest podzbiorem prostej rzeczywistej, zaś parametr t interpretuje się jako czas. Wówczas taką funkcję losową nazywamy procesem losowym lub procesem stochastycznym. Najczęściej stosujemy następujące oznaczenia:

Z pewnego punktu widzenia jest to jedna, ale wielowymiarowa zmienna losowa - jeśli mamy na myśli fakt, że ów ciąg zmiennych interpretujemy jako tę samą wielkość (np. cenę akcji czy poziom opadów), tyle że w różnych momentach. Formalnie w każdej z tych chwil postrzegamy ową zmieniającą się wielkość jako odrębną zmienną losową.

Intuicja odnosząca się do wektora losowego pozwala nam mówić o jego rozkładzie:

Możemy ustalić pewną "ścieżkę rzeczywistości", np. rozważyć konkretny scenariusz, w którym cena akcji w chwili t₁ wynosi 5 zł, w chwili t₂ jest to już 5,20 zł, w t₃ spada do 4,60 zł - i tak dalej. Będzie to tzw. szereg czasowy, czyli realizacja procesu stochastycznego:

Taką realizację określa się również jako funkcję próbkową lub trajektorię. To już nie jest funkcja losowa: bo "wylosowaliśmy" konkretny scenariusz. To, jak faktycznie ukształtował się kurs akcji - to szereg czasowy. To, jak mógł się ukształtować w zgodzie z cechującym go rozkładem prawdopodobieństwa - to proces stochastyczny.

Procesy stochastyczne można dzielić według różnych kryteriów. Dwa podstawowe to dyskretność i ciągłość, przy czym mogą się one odnosić tak do czasu, jak i do wartości samej zmiennej losowej. Istnieją zatem cztery kombinacje:

1) procesy dyskretne (skokowe, o przeliczalnym zbiorze wartości):

- w czasie dyskretnym
- w czasie ciągłym

2) procesy ciągłe

- w czasie dyskretnym
- w czasie ciągłym

Do tego jeszcze wrócimy. Na razie powiemy jeszcze o charakterystykach, pod kątem których można badać procesy losowe. W pierwszym rzędzie mamy wartość oczekiwaną procesu Y_t, czyli funkcję:

Innymi słowy, w danym momencie wartością tej funkcji jest po prostu wartość oczekiwana zmiennej losowej w czasie t. Naturalnie pytać można również o wariancję, tj. o funkcję:

Definicja ta nie jest zbyt zaskakująca. Krok trzeci to funkcja kowariancyjna procesu stochastycznego Y_t:

Definiowana jest następująco:

Warto przy tym odnotować następującą zależność:

Dalsza rzecz to tzw. unormowana funkcja kowariancyjna procesu:

Wróćmy do kwestii podziału procesów na kategorie. Otóż kryterium może być również tzw. stacjonarność. Wyróżniamy stacjonarność słabą i ścisłą, a także procesy niestacjonarne.

Proces losowy jest stacjonarny w sposób ścisły (tj. w węższym sensie), jeśli jego skończenie wymiarowe rozkłady nie zmieniają się przy przesunięciu parametru t o dowolną liczbę rzeczywistą h, a zatem (dla dowolnych t₁, ..., t_n, h należących do T):

Można więc powiedzieć, że zmienne losowe (Y₁, ..., Y_tn) oraz (Y_1+h, ... Y_tn+h), h>0, mają taki sam rozkład. Mamy także stacjonarność w szerszym sensie (słabą), a zachodzi ona wtedy, gdy:

1)

2)

3) poniższa kowariancja:

nie zależy od t (tj. od czasu).

A zatem w szczególności wartość oczekiwana i wariancja powinny być stałe. Intuicyjnie rzecz biorąc, wykres procesu stacjonarnego nie wybiega zanadto poza pewien obszar, krążąc niejako wokół średniej wartości. Nawiasem mówiąc, proces stacjonarny w szerszym sensie nie musi być stacjonarny w węższym. Odwrotna zależność zachodzi, o ile E(Y_t²) < ∞.

Wiele ważnych klas procesów (np. Poissona, gamma, Cauchy'ego, Wienera) to szczególne przypadki rozległej rodziny procesów Levy'ego. Te zaś definiowane są poprzez następujące własności:

1)

2) dla każdego ciągu 0 ≤ t₁ ≤ t₂ ≤ ... ≤ t_k zmienne losowe

są niezależne (a zatem jest to niezależność przyrostów procesu na rozłącznych odcinkach czasowych),

3) rozkład poniższy:

nie zależy od s (dla każdych s, t nie mniejszych niż 0),

4) proces jest ciągły według prawdopodobieństwa, tzn.:

Wspomnieliśmy o procesie Poissona. Otóż jest to proces o przyrostach niezależnych, taki że

zachodzą warunki:

1)

2) poniższe zmienne:

są niezależne, o wartościach całkowitych i nieujemnych,

3)

Jest to proces skokowy mierzony w czasie dyskretnym. Rozważmy zatem przykłady procesów, które są ciągłe, ale też w czasie dyskretnym. Dwie najbardziej znane klasy to białe szumy i procesy Markowa. Biały szum to proces ε_t o jednakowym rozkładzie (tj. w każdym momencie zmienna losowa ma taki sam rozkład) i zarazem taki, że dla wszystkich t:

1)

2)

3)

Jest to proces stacjonarny w węższym i szerszym sensie. Często zakłada się, że jego rozkład jest normalny i wtedy mówimy o tzw. gaussowskim białym szumie.

Proces Markowa ma do siebie to, że jego przyszłość zależy wyłącznie od teraźniejszości, a nie od przeszłości, zatem:

W zasadzie czas w procesie Markowa nie musi być mierzony dyskretnie, ale jeżeli tak jest, tj. gdy T składa się tylko z liczb całkowitych (albo jest z nimi równoliczny), to mówimy o łańcuchach Markowa. W szczególności bada się też dyskretne łańcuchy Markowa - w których także wartości zmiennej losowej przyjmują wartości jedynie ze zbioru przeliczalnego albo nawet skończonego (jak w procesach Poissona).

Następna rzecz to procesy Wienera (procesy ruchów Browna). Tego typu proces oznacza się jako W(t), przyjmuje on wartości z obszaru [0, 1], a do tego żąda się następujących własności:

1)

2) Dla wszystkich 0 ≤ t₁ ≤ t₂ ≤ ... ≤ t_k ≤ 1 przyrosty

są niezależnymi zmiennymi losowymi,

3)

To ostatnie oznacza, że zmienna W(s+t) - W(s) ma rozkład normalny. Proces Wienera opisuje (w przybliżeniu) ruch molekuły, która na swej drodze zderza się z innymi cząsteczkami; stąd też nawiązanie do słynnych ruchów Browna. W szczególności rozważa się często przypadek rozkładu normalnego o wariancji równej 1.

Przedstawimy jeszcze trzy tzw. autoregresyjne, liniowe modele procesów stacjonarnych: AR, MA i ARMA. Liniowe modele procesów niestacjonarnych (np. ARIMA, SARIMA) pominiemy, podobnie jak modele nieliniowe (ARCH, GARCH). W każdym razie liniowe modele autoregresyjne traktują wartość oczekiwaną procesu jako sumę bezwarunkowej wartości oczekiwanej niezależnej od czasu oraz warunkowej wartości oczekiwanej, która jest w sposób liniowy zależna od przeszłości.

Spójrzmy na wzór procesu typu AR(p) - czyli autoregresyjny rzędu p:

Mamy tu: μ - tj. stałą wartość oczekiwaną (parametr ten bywa pomijany, tj. zerowany), następnie kombinację liniową wartości zmiennej losowej i pewnych parametrów Φ_i (są one liczbami), a na końcu biały szum, czyli zakłócenie, element chaotyczny. Zauważmy, że wartość procesu w czasie t (lewa strona równości) jest zależna od tego, co działo się we wcześniejszych momentach.

MR(q) - czyli moving average rzędu q - to proces średniej ruchomej:

Konstrukcja jest podobna do AR(p), ale tym razem mamy kombinację liniową wartości szumu. Sumować można w nieskończoność, co jest o tyle istotne, że każdy szereg typu AR(1) można zapisać przy pomocy szeregu typu MA(∞), czego jednak nie będziemy dowodzić.

Ostatnia rzecz to procesy typu ARMA(p,q). To połączenie AR i MA, jak zresztą łatwo się domyślić. Wzór prezentuje się następująco:

Na koniec (który tak naprawdę powinien być dla czytelnika dopiero początkiem, vide choćby bibliografia) raz jeszcze podkreślmy istotność procesów stochastycznych. Są stosowane zarówno w ekonomii (przy modelowaniu takich zjawisk jak zmienność kursu instrumentów finansowych, wielkości makroekonomicznych czy wypłaty z tytułu ubezpieczenia), jak i fizyce, chemii czy biologii.

Adam Witczak

BIBLIOGRAFIA:

A. Ganczarek-Gamrot, "Analiza szeregów czasowych", Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2014

T. Kufel, "Postulat zgodności w dynamicznych modelach ekonometrycznych", Wydawnictwo UMK, Toruń 2002.

D. Bobrowski, "Modele i metody matematyczne teorii niezawodności", WNT 1985

A. D. Wentzell, "Wykłady z teorii procesów stochastycznych", PWN 1980