Nie kończąca się historia - cz. II

Zgodnie z tym, co zapowiedzieliśmy, dowiedziemy teraz, że na płaszczyźnie odcinek jest równoliczny z kwadratem. W istocie jest to fakt, który powinien nas zadziwiać, choć być może czysto formalne spojrzenie na matematykę stępiło przez ostatnich sto lat naszą wrażliwość. Przedstawimy najpierw bardzo "poglądowe" rozumowanie, później zaś ścisłe rozumowanie wskazujące, że moc zbioru liczb rzeczywistych równa jest mocy płaszczyzny.

Mamy zatem kwadrat, dla uproszczenia – jednostkowy (tj. wyznaczony przez punkty (0, 0), (0, 1), (1, 0) i (1, 1)). Każdy jego punkt ma rzecz jasna dwie współrzędne: x i y. Co za tym idzie, możemy zastosować, podobnie jak czyniliśmy to przy dowodzie nieprzeliczalności zbioru liczb rzeczywistych, następujący zapis:

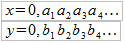
Zakładamy przy tym stosowanie jednoznacznego zapisu, tj. np. przyjmujemy 0,24999... - a nie 0,25000... (moglibyśmy zrobić odwrotnie, to wybór czysto arbitralny). Teraz chcemy każdej takiej wyżej opisanej parze <x, y> przypisać pojedynczy punkt na odcinku [0, 1]. Bardzo proszę:

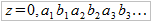
Jak widać, rozwinięcie dziesiętne naszej nowej liczby zawiera naprzemiennie ułożone wyrazy rozwinięć dziesiętnych liczb x i y. Jeśli więc w kwadracie natrafimy na punkt o współrzędnych (0,454545..., 0,34212293...) - to przypiszemy mu z postaci 0,4354425142...

Opisane wyżej przyporządkowanie nie powinno nas w pełni satysfakcjonować. Na pierwszy rzut oka wszystko jest w porządku. Okazuje się jednak, że podana funkcja nie jest "na", tzn. że dla niektórych punktów na odcinku nie znajdziemy odpowiedników w kwadracie.

Weźmy np. na odcinku liczbę 0,37909090909... Jaki punkt w kwadracie jej odpowiada? Wydaje się, że odpowiedź jest oczywista: taki, którego x to 0,399999..., zaś y to 0,700000... Wiemy jednak, że 0,700000 to w istocie 0,699999..., a taki zapis postanowiliśmy wybrać. A zatem x to 0,399999..., zaś y to 0,699999... Zauważmy jednak, że punktowi o takich współrzędnych nie odpowiada liczba 0,3790909..., ale 0,36999... - zupełnie inna. Owszem wykorzystujemy wszystkie punkty kwadratu, ale na odcinku nie trafiamy we wszystkie liczby.

Zmienimy nieco nasze podporządkowanie – i mieszać będziemy nie pojedyncze cyfry, a ich grupy – kilka cyfr z x, kilka z y itd. Oczywiście nie w sposób bezmyślny.
Otóż podzielimy nasze rozwinięcia na bloki cyfr cechujące się tym, że każdy blok zawiera następujące kolejno po sobie zera i pierwszą cyfrę niezerową włącznie z nią. Jeśli kolejna cyfra jest niezerowa, to utworzy ona blok jednocyfrowy. Jeśli nastąpi po niej np. pięć zer i cyfra niezerowa – to właśnie ten zestaw będzie kolejnym wyróżnionym blokiem. Przykładowo liczbę 0,0945000100209765003... dzielimy następująco:

0,  09  4  5  0001  002  09  7  6  5  3  003 ...

Tak postępujemy ze współrzędnymi x i y punktów w kwadracie. Teraz przy konstrukcji liczby na odcinku będziemy naprzemiennie układać takie właśnie bloki. Np. dla x = 0,0024303... i y = 0,123304... dostaniemy z = 0,  002  1  4  2  3  3  03  04, tj. z = 0,002142330304...

Wróćmy teraz na moment do naszego przykładu z liczbą 0,37909090909... z odcinka. Co jej odpowiada w kwadracie według naszej nowej funkcji? Otóż będzie to punkt (x, y) taki, że x = 0,3909090909..., zaś y = 0,709090909... Dwuznaczność zniknęła, nie zdarzy się nam już "zapętlenie zer" po drugiej stronie. Oczywiście to nie jest formalny dowód, a tylko przykład działania nowej funkcji. Formalny zapis nie byłby zbyt trudny, ale nie byłby też ciekawy.

A teraz pokażemy, że zbiór wszystkich podzbiorów danego zbioru A ma większą moc niż A. Innymi słowy, jeśli A ma pewną liczbę elementów, to wszystkich możliwych podzbiorów A jest więcej niż tych elementów.

Przyjmijmy oznaczenie, w myśl którego P(A) to zbiór wszystkich podzbiorów A. Wyjaśnijmy na przykładzie, co to znaczy. Jeśli np. A jest skończony i wygląda tak: {1, 2, 3}, a więc składa sięz trzech liczb, to P(A) = { {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}, zbiór pusty }. Zbiór pusty jest podzbiorem każdego zbioru – ostatecznie przecież każdy jego element (czyli żaden, bo pusty nie posiada elementów) jest zarazem elementem A. Również sam zbiór A traktujemy jako swój własny podzbiór – można bowiem rzec, że "wszystkie jego elementy są elementami A, tj. jego samego", a więc spełnia definicję podzbioru. Zarówno jednak zbiór pusty, jak i cały A określamy jako podzbiory niewłaściwe, właściwymi są te, w których zawarte są nie wszystkie elementy A. Podkreślmy też, że element 3 to nie to samo, co {3} – w tej drugiej formie zapisujemy zbiór (podzbiór A), który zawiera jeden element, a jest nim właśnie 3. Taki zbiór jednoelementowy fachowo zwie się singletonem danego elementu.

Załóżmy nie wprost, że B ma moc mniejszą lub równą niż A, to znaczy, że jest w nim tyle elementów, co w A – albo mniej. To znaczy, że istnieje pewna funkcja:

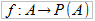
Funkcja ta jest (musi być, jak już wiemy) bijekcją, to znaczy jest równocześnie różnowartościowa i "na". Przyporządkowuje ona każdemu elementowi A pewien podzbiór A. W naszym przykładzie mogłoby to np. oznaczać, że liczbę 3 łączymy z podzbiorem {1, 2} - albo z singletonem trójki, czyli {3}. Albo z innym podzbiorem A.

Naszym celem jest pokazanie, że tak naprawdę takiej funkcji nie ma, a żeby to zrobić, wskażemy pewien element zbioru P(A) – a więc pewien podzbiór A – dla którego "po drugiej stronie", tj. w A, z pewnością nie ma odpowiednika. Coś podobnego robiliśmy parę chwil temu przy okazji odcinka i kwadratu.

Zdefiniujmy teraz zbiór Z jako:

Zapis ten może być niejasny. Otóż jeśli elementowi zbioru A przypisujemy podzbiór zbioru A, to możemy wybrać taki podzbiór, w którym ten element się znajduje lub taki, w którym go nie ma. Czytelnik zapewne sięga teraz wzrokiem kilka akapitów wyżej. Tak, trójce ze zbioru {1, 2, 3} możemy przypisać podzbiór, w którym ona jest (np. {3} albo {2, 3}) lub taki, w którym jej nie ma – np. {1} lub {1, 2}. Zbiór Z gromadzi zatem takie elementy A (takie "iksy"), które nie należą do przypisanych im podzbiorów. A więc jeśli liczbie 3 odpowiadałby zbiór {2}, to liczba 3 byłaby elementem Z.

Z zawiera elementy zbioru A, jest więc podzbiorem A – czyli elementem P(A). Przypomnijmy tu i podkreślmy, że elementami P(A) są podzbiory A – to niezwykle ważne, by odróżniać od siebie A i P(A). Wróćmy jednak do toku rozumowania. Skoro Z jest podzbiorem A, to istnieje taki element a należący do A, któremu przez funkcję f przypisany jest właśnie Z:

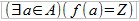
Rodzi się pytanie o to, czy a należy do samego Z. To bardzo ciekawe pytanie, ponieważ obie możliwe odpowiedzi prowadzą do sprzeczności:

- załóżmy, że a należy do Z, jest jego elementem. To jednak niemożliwe, bo Z zawiera tylko te elementy, które nie należą do "swoich" podzbiorów. Tymczasem "podzbiorem dla a" jest właśnie Z.

- załóżmy, że a nie należy do Z. To nam nie pomoże, bo jeśli a nie należy do zbioru, który został mu przyporządkowany, to znaczy, że spełnia warunek należenia do Z. Należy więc do Z.

Czyli: jeśli należy, to nie należy, a jeśli nie należy, to należy. Jest to sprzeczność, a nawet dwie sprzeczności. Rezultat rozumowania pokazuje nam, że błędne było nasze pierwotne założenie, iż może istnieć bijekcja przeprowadzająca A na P(A).

Wróćmy tymczasem na moment do pierwotnej wersji naszego przyporządkowania. Dzięki niej dowiedzieliśmy się, że w kwadracie nie ma więcej punktów niż na odcinku. Oczywiście nie jest ich też mniej (choćby dlatego, że odcinek sam należy w całości do kwadratu). Formalnie znaczy to, że moc kwadratu jest mniejsza lub równa od mocy odcinka – i zarazem moc odcinka jest mniejsza lub równa od mocy kwadratu. Intuicyjnie wnioskujemy z tego, że moce obu zbiorów są równe.

Ta intuicja mogłby jednak okazać się zwodnicza. Na szczęście nie jest, o czym mówi twierdzenie Cantora-Bernsteina, o którym za chwilę. Mamy tu na myśli to, że przecież, jak zdążyliśmy się przekonać, świat zbiorów nieskończonych obfituje w pewne paradoksy. Liczb całkowitych i wymiernych jest tyle samo, co naturalnych, na najmniejszym odcinku jest tyle samo liczb, co na całej prostej – itd. Nie możemy odruchowo, bezkrytycznie traktować mocy zbiorów nieskończonych tak, jak zwyczajnych liczb.

Twierdzenie Cantora-Bernsteina, jak wstępnie zasugerowaliśmy, mówi rzecz następującą: jeśli moc A jest mniejsza lub równa od mocy B, ale jednocześnie moc B jest mniejsza lub równa od mocy A, to moce obu tych zbiorów są takie same. Można formułować twierdzenie również i tak: jeśli A zawiera się w B, zaś B zawiera się w C, a jednocześnie A ma tyle elementów, co C (jest równoliczny z C), to wówczas B też jest równoliczny z C.

Dowód tego twierdzenia jest wbrew pozorom bardzo złożony i dlatego nie będziemy go przytaczać w tekście, który ma ambicję być popularnym oraz skierowanym raczej do laików. Nie znaczy to, by dowód ten wykorzystywał jakieś pojęcia znacznie bardziej zaawansowane od już omówionych – faktem jest jednak, że opiera się na pewnych "chwytach", które należałoby bardzo precyzyjnie i powoli omówić. Dowód oczywiście bez problemu znajdziemy w każdej chyba książce na temat teorii zbiorów (lub w pracach obejmujących uniwersytecki kurs "wstępu do matematyki", na który zwykle składają się elementy logiki i właśnie teorii zbiorów).

Naszym celem było przede wszystkim zupełnie wstępne zapoznanie Państwa z intrygującymi faktami, na jakie natrafiamy, gdy zaczynamy rozmyślać o nieskończoności. Faktów tych jest w istocie nieskończenie wiele... a my jesteśmy na razie dopiero na skraju ogromnej przestrzeni. Mieliśmy jednak także i drugi cel - zapoznać Czytelnika z pewnymi procedurami definiowania i dowodzenia, które stosowane są w matematyce. Staraliśmy się przy tym zachować formę możliwie popularną, jednocześnie jednak unikając sprowadzania wszystkich kwestii do atrakcyjnych być może, ale niewiele mówiących banałów. Pozostaje mieć nadzieję, że opłacił się zarówno nasz wysiłek, jak i wysiłek umysłowy szanownych Czytelników.

Adam Witczak