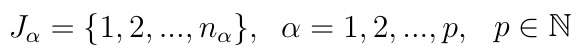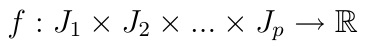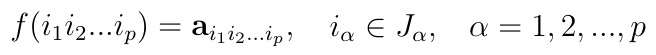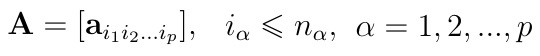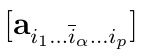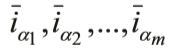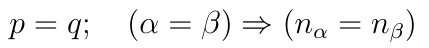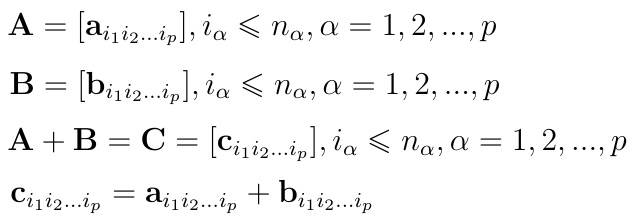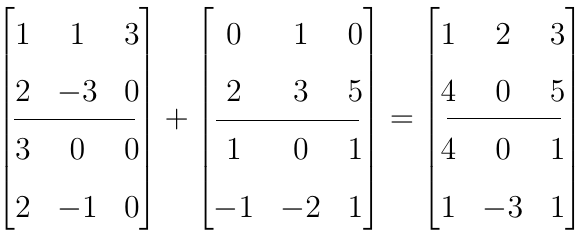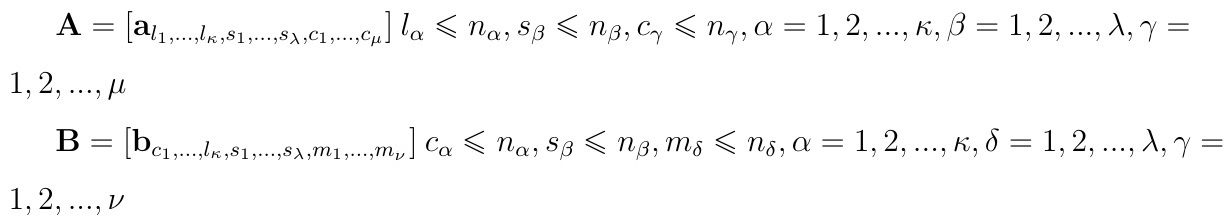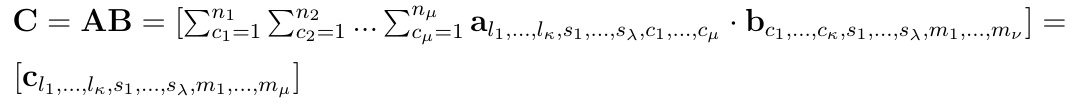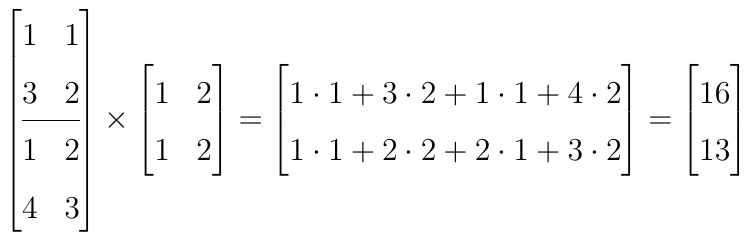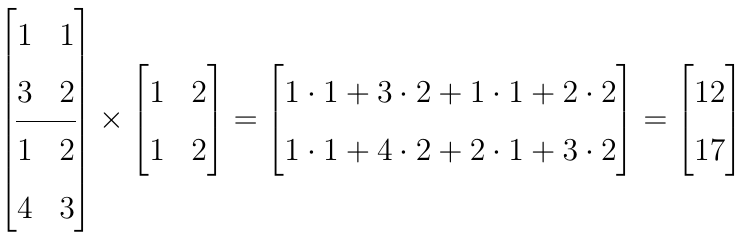Macierze wielowskaźnikowe

W zasadzie każdy, kto uczęszczał na studia ekonomiczne, miał do czynienia z macierzami - choćby w ramach elementarnego kursu algebry liniowej. Oczywiście ta uwaga dotyczy także (albo i jeszcze bardziej) absolwentów kierunków inżynierskich, nie mówiąc o fizyce, matematyce i informatyce.

W ramach algebry liniowej niemal zawsze omawia się macierze (ew. krakowiany) dwuwymiarowe: to znaczy takie, które składają się tylko z wierszy i kolumn, a więc każdy wyraz ma jedynie dwie współrzędne, co zapisuje się np. jako a₁₂ czy a₃₄ (ogólnie a_ij).

Dziś jednak będziemy mówić o macierzach wielowymiarowych czy też wielowskaźnikowych. W tych obiektach każdy element ma więcej niż dwie współrzędne - np. 3, 4, 5 lub jeszcze więcej. W pewnym sensie są to obiekty zupełnie naturalne, bo przecież często spotykamy się z klasyfikacją rzeczy ze względu na kilka kryteriów. A jednak teoria macierzy wielowskaźnikowych jest jeszcze stosunkowo młoda i mało znana: głównie dlatego, że bez programu komputerowego wszelkie obliczenia, a nawet same definicje, jawią się jako skomplikowane i niekoniecznie intuicyjne (o czym się zaraz przekonamy).

*

Podążać będziemy przede wszystkim za artykułami J. Olesinkiewicza i W. Sklinsmonta. Z nich zaczerpniemy notację i niektóre przykłady. Zaczniemy od podstawowych, formalnych definicji.

Rozważmy następujące, skończone podzbiory zbioru liczb naturalnych:

Na przykład J₁ = {1, 2, 3}, J₂ = {1, 2}, wówczas n₁ = 3 dla α= 1, n₂ = 2 dla α= 2, zaś p = 2.

Poniższą funkcję:

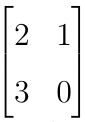
- nazywamy p-wskaźnikową macierzą o wartościach rzeczywistych. Prosty przykład to 2-wskaźnikowa macierz 2 na 2. Przyjmujemy p = 2, n₁ = 2, n₂ = 2. Funkcja staje się wówczas przypisaniem czterech wartości do dwóch kolumn i dwóch wierszy, choćby w taki sposób:

Jeśli weźmiemy pierwszy element zbioru J₁ i pierwszy element J₂, to odpowiada mu lewy górny wyraz tej macierzy. Jego wartość to, jak łatwo zauważyć, 2. A więc 2 to w tym wypadku wartość funkcji f.

Oczywiście tak naprawdę będą nas interesować głównie macierze o p większym niż 2.

Taką liczbę:

- nazywamy elementem p-wskaźnikowej macierzy (element ten ma współrzędne i₁ i₂ ... i_p). W podanym przed chwilą przykładzie element o współrzędnych i₁ = 2, i₂ = 1, to element z 2-go wiersza i 1-szej kolumny (jeśli indeksem i₁ odliczamy wiersze, a przy pomocy i₂ kolumny), czyli wyraz 3 (lewy dolny róg).

Całą macierz, tj. zbiór wartości funkcji f, symbolicznie zapisujemy jak poniżej:

Nazywa się to obrazem p-wskaźnikowej macierzy. Liczbę n_α nazywamy stopniem wskaźnika i_α. W naszym przykładzie mamy 2-wskaźnikową macierz 2 na 2, czyli dla obu wskaźników, tj. dla wierszy i kolumn, stopień jest taki sam i wynosi 2. W macierzy 2-wskaźnikowej, ale 3 na 4 (trzy wiersze i cztery kolumny), mielibyśmy stopnie 3 i 4.

*

Następna rzecz, zresztą bardzo istotna, to tzw. przekrój prosty o orientacji i_α. Symboliczny zapis jest taki:

Oznacza to, że ustalamy wartość współrzędnej i_α i dostajemy macierz p-1 wskaźnikową. Można też ustalić więcej wartości indeksów:

- i otrzymać macierz (p-m)-wskaźnikową. Brzmi to bardzo niejasno, dlatego rzecz warto zobaczyć na przykładzie. W operacji tej chodzi o to, że przy pomocy (p-1) lub (p-2)-wskaźnikowych przekrojów można nawet bardzo wielowymiarowe macierze zapisywać przy pomocy tablic prostokątnych.

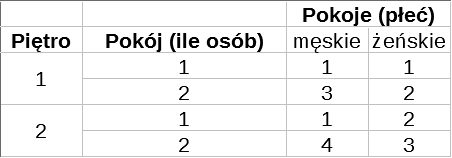
Spójrzmy:

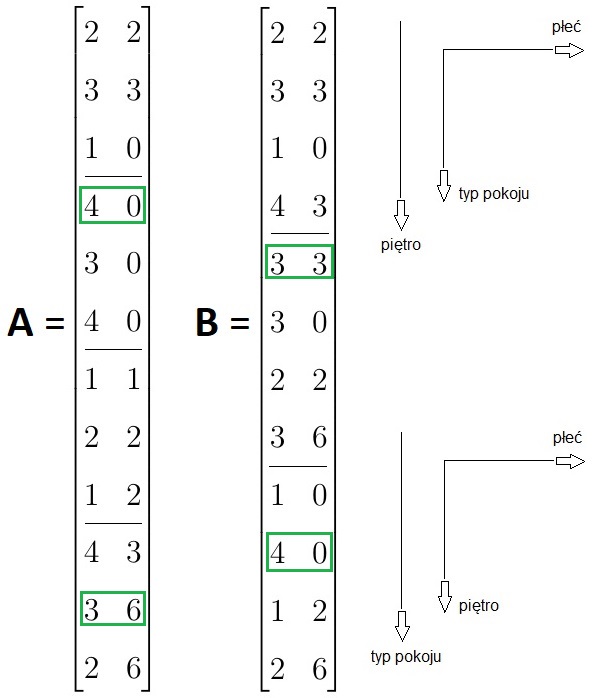
Mamy tu macierz A (zaczerpniętą z publikacji Olesinkiewicza), którą należy czytać następująco: cztery "klatki" (zamiennie będziemy używać słów takich jak "kratki" lub "bloki") ułożone pionowo odpowiadają piętrom w akademiku; następnie wewnątrz każdej klatki kolumna mówi nam, ile pokojów danego typu jest na piętrze (chodzi o pokoje 1-, 2-, 3-osobowe, to już wiedza zewnętrzna, nie wynikająca z macierzy); a wiersz mówi nam, ile jest pokojów dla danej płci (męskiej i żeńskiej). Na przykład na drugim piętrze mamy 4 jednoosobowe pokoje męskie i 0 damskich tego typu. Z kolei na czwartym piętrze mamy 3 dwuosobowe pokoje męskie i 6 damskich tego rodzaju.

Jest to przekrój typu p-1: wybraliśmy współrzędną odpowiadającą piętrom i patrzymy, jak wyglądają sprawy na piętrach.

Ale macierz B, również w przekroju typu p-1, odnosi się do tego samego obrazu. Tym razem wybieramy jednak współrzędną określającą typ pokoju. Zatem są trzy klatki: pokoje 1-, 2- i 3-osobowe. Za to każda klatka ma 4 wiersze (cztery piętra) i 2 kolumny (płci, podobnie jak poprzednio). W ten sposób możemy np. łatwo dowiedzieć się, że jeśli chodzi o pokoje 3-osobowe, to na drugim piętrze są 4 męskie tego typu i zero damskich, a jeśli chodzi o pokoje 2-osobowe, to na pierwszym piętrze są po 3 męskie i damskie.

Następny obraz cytujemy za pracą Sklinsmonta:

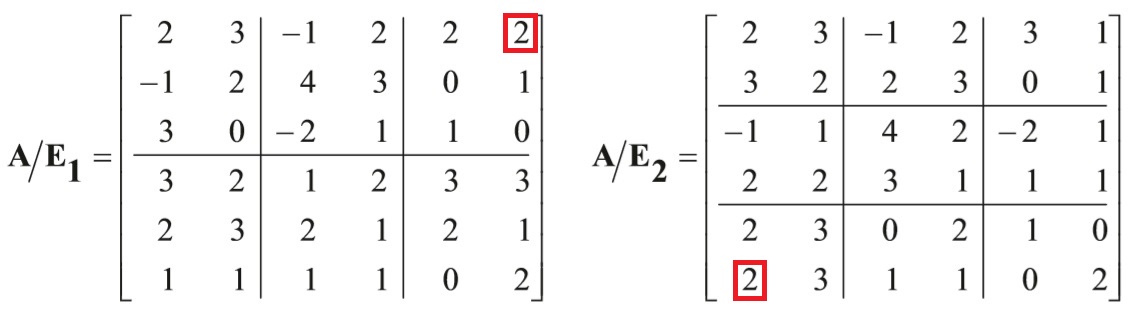
Tutaj pokazane są dwie struktury zapisu pewnej macierzy A, 4-wskaźnikowej. Strukturę taką symbolicznie oznaczamy jako E (w tym wypadku E₁ i E₂). Struktury nie zawierają właściwych danych macierzy, a jedynie współrzędne tych danych (elementów). Pierwsza struktura, E₁, powinna być interpretowana tak: "kratki" poziomo to współrzędna i₄, kratki pionowo to wskaźnik i₃, a w każdej kratce wybieramy indeks i₁ jako wiersz oraz i₂ jako kolumnę. Przykład: w prawym dolnym rogu mamy element o współrzędnych 3223, tj. 3-ci wiersz, 2-ga kolumna, 2-gi rząd kratek i 3-cia kolumna kratek.

Zapis E₂ jest inny: tym razem nasze "główne", przekrojowe współrzędne to i₁ w poziomie (trzy kolumny kratek) i i₄ w pionie (trzy wiersze kratek), a w każdej kratce mamy jeszcze dwa wiersze (indeks i₂) i dwie kolumny (indeks i₄).

Konkretna macierz A zapisana na te dwa sposoby może wyglądać tak:

Rozważmy element w prawym górnym rogu A/E₁. Ma on wartość 2 oraz indeks 1213: pierwszy wiersz i druga kolumna wewnątrz kratki, a kratka ta jest położona w pierwszym rzędzie i trzeciej kolumnie kratek. Element ten w zapisie A/E₂ trafia do lewego dolnego rogu całej macierzy!

*

Dwie macierze wielowskaźnikowe są tego samego typu, jeśli:

To znaczy, że: 1) mają tyle samo wskaźników; 2) a odpowiadające sobie wskaźniki są tego samego stopnia. Możemy je wówczas dodawać:

To działanie nie jest skomplikowane, dodaje się po prostu odpowiadające sobie elementy:

W tym wypadku dodajemy dwie macierze 3-wskaźnikowe, przy czym jeśli "kratki" czy też "bloki" indeksować jako i₁, to i₁ jest stopnia 2 (dwie kratki), a jeśli wewnątrz "bloku" i₂ to wiersze, zaś i₃ to kolumny, wtenczas i₂ jest stopnia 2, a i₃ stopnia 3.

*

Dodawanie jest proste. Znacznie bardziej skomplikowane jest mnożenie, które naprawdę przyprawiać może o ból głowy - przynajmniej wtedy, gdy próbujemy literalnie stosować ogólne wzory.

Zacznijmy od tego, że indeksy naszej macierzy, tj. ciąg i₁ i₂ ... i_p rozbijamy na trzy rozłączne ciągi (bloki), być może zmieniając kolejność. Zapisujemy to symbolicznie jako l₁, ..., l_κ, s₁, ... s_λ, c₁, ..., c_μ. Dla dwóch macierzy A i B powinno to wyglądać tak:

Obowiązują przy tym zależności κ + λ + μ = p oraz λ+ μ+ ν= q. Iloczyn macierzy A i B określa się tak:

Wzór jest trudny, może wręcz koszmarny: przy większych rozmiarach ręczne obliczenia są z tego powodu żmudne i nieoczywiste. W dodatku procedura ta nie jest jednoznaczna, tzn. zależy ona od sposobu rozbicia naszych pakietów indeksów. Wynikowa macierz ma zawsze κ + λ + ν wskaźników, przy czym niektóre z tych liczb mogą być zerowe.

Zobaczmy zatem, jak to działa - na pewnym prostym przykładzie, który okaże się mocno intuicyjny. Jest to uproszczony wariant wcześniejszego modelu domu studenckiego.

Spójrzmy:

Mamy dom studencki o dwóch piętrach, z pokojami 1- i 2-osobowymi, a zarazem z pokojami męskimi i damskimi. Załóżmy, że wszystkie pokoje są zajęte. Ilu jest mężczyzn, a ile kobiet w budynku?

Intuicja podpowiada, że powinniśmy przejść przez oba piętra i na każdym zliczać mężczyzn (liczba męskich pokoi danego typu razy liczba osób w takim pokoju), a równolegle wykonywać analogiczny rachunek dla kobiet. Rzeczywiście. Jako iloczyn macierzy zapisać możemy to następująco:

W pierwszym wierszu zliczamy mężczyzn, najpierw z pierwszego piętra (1*1 + 3*2), potem z drugiego (1*1 + 4*2), w drugim sumujemy damy.

Gdybyśmy przyjrzeli się temu działaniu i uważnie porównali je z ogólnymi wzorami zaprezentowanymi wyżej, to przekonalibyśmy się, że wszystko jest zgodne z tymi formułami.

A teraz mała zmiana: pytamy, ile osób (niezależnie od płci) jest na każdym piętrze. Czyli idziemy na pierwsze piętro, zliczamy mężczyzn i kobiety (na podstawie wiedzy o liczbie i liczebności pokojów), zapamiętujemy wynik - i przechodzimy na piętro drugie. Wygląda to tak:

Najpierw bierzemy kolumnę lewą górnej "kratki" naszej macierzy i dokonujemy jej "sumomnożenia" przez pierwszy wiersz drugiej macierzy; potem bierzemy prawą kolumnę górnej "kratki" i znów pierwszy wiersz drugiej macierzy (co prawda jej wiersze są akurat takie same...). Wyniki te sumujemy i dostajemy 12. Zmieniamy "kratkę" na dolną i postępujemy analogicznie.

Powiedzmy raz jeszcze: mamy w obu przykładach te same macierze, ale mnożymy je według innych reguł. Autorzy, których cytujemy, wyliczają aż 13 możliwości takiego mnożenia i podają dodatkowe warunki wykonalności. Stosując różne rozbicia indeksów można uzyskiwać analogony mnożeń znanych ze świata macierzy dwuwymiarowych, czyli np. iloczynu Hadamarda, iloczynu Kroneckera, produktu Khatri-Rao lub zwykłego iloczynu macierzy. Jedną z opcji jest również iloczyn tensorowy.

Macierze wielowskaźnikowe mają faktyczne i potencjalne zastosowania w takich zagadnieniach jak wielokryterialne podejmowanie decyzji, rachunkowość czy bazy danych. Oczywiście w praktyce obliczenia wykonuje - według uprzednio napisanych algorytmów - komputer.

Adam Witczak


BIBLIOGRAFIA:

H. J. Bao, A. J. Sang, H. X. Chen, "Inverse Operation of Four-Dimensional Vector Matrix", "I.J. Intelligent Systems and Applications", 2011, 5, 19-27.

J. Olesinkiewicz, "Macierze wielowskaźnikowe jako instrument działań na strukturach danych", w: "Metody matematyczne, ekonometryczne i informatyczne w finansach i ubezpieczeniach", cz. 2, red. P. Chrzan, Wyd. Akademii Ekonomicznej w Katowicach 2006.

W. Sklinsmont, "Macierze wielowskaźnikowe w naukach ekonomiczno-społecznych", Acta Universtiatis Lodziensis, Folia Oeconomica, 253, 2011.

Ashu M. G. Solo, "Multidimensional Matrix Mathematics: Multidimensional Matrix Transpose, Symmetry, Antisymmetry, Determinant and Inverse, part 4 of 6", Proceedings of the World Congress on Engineering 2010 Vol III WCE 2010, June 30 - July 2, 2010, London, U.K.