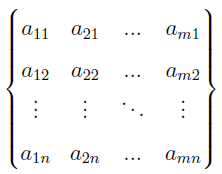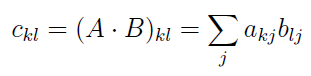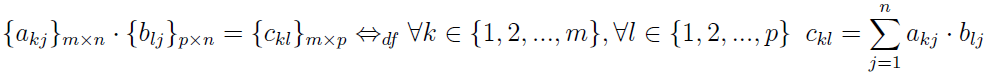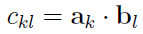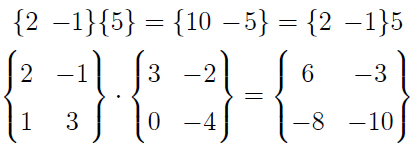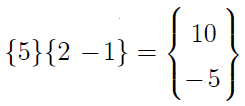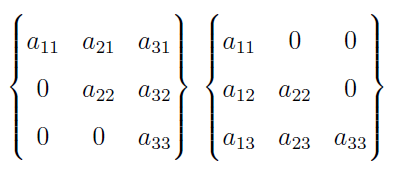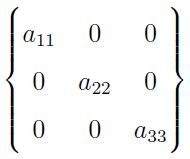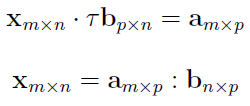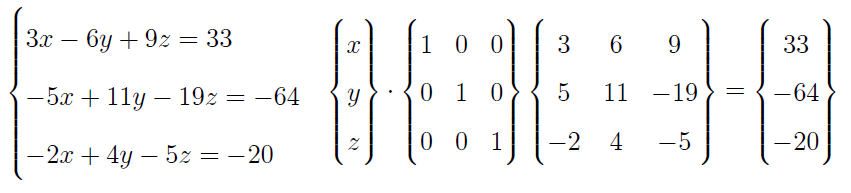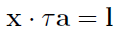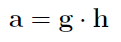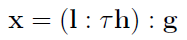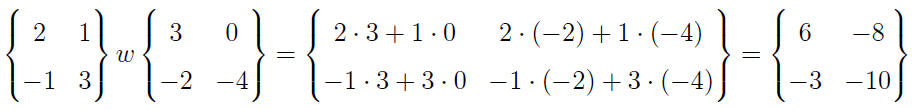Rachunek krakowianowy

Rachunek krakowianowy to dziś trochę zapomniana gałąź matematyki. Jeżeli już się o nim wspomina, to raczej z wyraźną sugestią, że krakowiany to swego rodzaju gorsza wersja macierzy - narzędzie, które miało zastosowanie w krótkiej epoce mechanicznych i elektromechanicznych arytmometrów, ale w erze komputerów przestało być użyteczne.

W dużej mierze jest to prawda, ale nie do końca - choćby dlatego, że krakowiany, pojęte abstrakcyjnie, jako twór matematyczny, tworzą ciekawą algebrę, co tworzy łącznik pomiędzy nimi a nowoczesnymi działami matematyki wyższej. Świadczy o tym np. materiał zawarty w książce 'Cracovian Algebra' J. Kocińskiego.

Teoretycznie można sobie też wyobrazić ekonomiczne zastosowanie krakowianów - przede wszystkim ze względu na ich rolę w rozwiązywaniu układów równań liniowych, a także ze względu na krakowianową interpretację metody najmniejszych kwadratów. Tę metodę stosuje się np. w ekonometrii czy przy konstrukcji wskaźników analizy technicznej. Co więcej, krakowiany były - i do pewnego stopnia nadal są - popularne w geodezji. Ta zaś w naturalny sposób wiąże się z ekonomią. Na niektórych uczelniach prowadzone są nawet kierunki czy specjalizacje, w których geodezję łączy się np. z zagadnieniem szacowania i wyceny nieruchomości.

Sama nazwa 'krakowian' pochodzi oczywiście od Krakowa, co rodzi podejrzenie, iż jest to twór rodzimy, polski. W istocie - tak właśnie jest. Twórcą metody krakowianowej był Tadeusz Banachiewicz (1882 - 1954), wybitny polski astronom i geodeta. Swoją koncepcję usilnie propagował on przez kilka dekad, przy czym nierzadko spotykał się z nieufnością matematyków. Część z nich uważała bowiem krakowiany za narzędzie zbędne z czysto matematycznego punktu widzenia. Tym niemniej wynalazek Banachiewicza przyjął się w zastosowaniach praktycznych i przez kilka dekad wykładano go na uczelniach technicznych, jak również poświęcono mu trochę miejsca w podręcznikach dla inżynierów i astronomów.

Ba, w roku 1957 zbudowano nawet specjalną maszynę do wykonywania obliczeń krakowianowych: PARK (Programowany Automat Rachunków Krakowianowych). Było to urządzenie dziś zaliczane do tzw. komputerów zerowej generacji. Jego serce stanowiła maszyna fakturująca, czyli rodzaj elektro-mechanicznego kalkulatora. Na tablicy połączeń ustawiało się program, który modyfikował zadany układ równań - aż do jego rozwiązania w kolejnych fazach. PARK był też wyposażony w trzy czytniki dalekopisowe do przyjmowania danych początkowych i prezentowania wyników. Maszynę wyprodukowano w Warszawie, a później przewieziono do Akademii Górniczo-Hutniczej w Krakowie.

(źródło: A. B. Empacher, Maszyny liczą same?, Wiedza Powszechna i Sztandar Młodych 1960)

Czym jest krakowian? Zakładamy, że czytelnik zna podstawy algebry liniowej i rachunku macierzowego, wykładane np. na każdym kierunku ekonomicznym. Spójrzmy więc na taki zapis:

Powyższy twór wygląda jak macierz, ale dwie rzeczy mogą nas dziwić. Po pierwsze, numeracja wyrazów wskazuje, że element a_kl to element w k-tej kolumnie i l-tym wierszu, odwrotnie niż w zapisie znanym z macierzy, gdzie najpierw podajemy wiersz, a potem kolumnę. Po drugie, tablica nie jest ograniczona nawiasami zwykłymi lub kwadratowymi, ale klamrowymi.

Czy to wszystko? Oczywiście nie. Naturalnie krakowian jest pod wieloma względami podobny do macierzy. Analogicznie przebiega działanie dodawania - po prostu dodajemy do siebie odpowiadające elementy, przy czym oba krakowiany muszą mieć takie same wymiary. Możemy też przemnożyć krakowian przez skalar - i wtedy każdy wyraz krakowianu jest mnożony; przy czym działanie to jest przemienne.

W czym więc tkwi różnica? Otóż w definicji mnożenia. Zakładamy, że czytelnik pamięta definicję mnożenia macierzy: jak to się zwykle mówi na wykładach, mnożymy każdy wiersz pierwszej macierzy przez każdą kolumnę drugiej. Jeśli A ma wymiary m x n, to B musi być postaci n x k, a wynikowa macierz C ma wymiary m x k.

W krakowianach mnożenie definiuje się inaczej, czego mankamentem jest fakt, że działanie to nie jest łączne. Czyli w ogólności nie musi być tak, że A(BC) = (AB)C. Z tego powodu algebra krakowianów nie jest grupą (jak algebra macierzy), a jedynie tzw. quasi-grupą (nie mylić z półgrupą, ang. semi-group). Mnożenie to nie jest poza tym przemienne (ale macierze też generalnie tego warunku nie spełniają).

W zapisie rzecz wygląda tak:

Bardziej szczegółowo zaś tak:

W skrócie mamy:

Co to znaczy? Otóż możemy mnożyć tylko takie krakowiany, które mają tyle samo wierszy (w drugim wzorze mają po n wierszy; pamiętajmy, że indeksy interpretujemy w odwrotnej kolejności niż w macierzach). Wynikowy krakowian ma tyle kolumn, co pierwszy czynnik - i tyle wierszy, ile drugi czynnik miał kolumn.

Element c_kl powstaje zatem przez przemnożenie elementów k-tej kolumny krakowianu a i l-tej kolumny krakowianu b, po wszystkich wierszach. Ale jak mnożyć kolumny?

Otóż pierwszy element pierwszej kolumny mnożymy przez pierwszy element drugiej - i do tego dodajemy analogiczny iloczyn obliczony wiersz niżej. I tak dalej - po wszystkich wierszach. Tak jak przy iloczynie skalarnym dwóch wektorów. Operację tę określa się czasami jako sumomnożenie.

Spójrzmy na przykłady:

Skąd wynik w pierwszej linijce? Bo 2*5 = 10, a -1*5 = -5. Nawiasem mówiąc, w tym wypadku mnożenie przez krakowian {5} jest tożsame z mnożeniem przez skalar.

W drugim przykładzie spójrzmy na lewy górny wyraz krakowianu wynikowego. To 6 = 2*3 + 1*0. Mnożymy przez siebie pierwsze kolumny. Z kolei w lewym dolnym rogu (liczba -8, pierwsza kolumna, drugi wiersz) mamy mnożenie pierwszej kolumny lewego czynnika i drugiej prawego. Istotnie: -8 = 2*(-2) + 1*(-4).

Wygląda to dziwnie, ale chyba nie jest trudniejsze niż mnożenie macierzy, a może i prostsze. Inna rzecz, że tak określone działanie generuje mocno odmienną algebrę, o czym już wspominaliśmy. Nie będziemy jednak zajmować się tą kwestią, a zamiast tego przedstawimy jeszcze jeden przykład mnożenia:

Duże znaczenie mają krakowiany szczególnej postaci. Są one w dużej mierze analogiczne do macierzy. Mamy więc krakowiany kwadratowe (Banachiewicz używał dość niecodziennego terminu "kwadraste"), czyli takie, gdzie liczba kolumn jest równa liczbie wierszy. Mamy krakowiany symetryczne, czyli takie kwadratowe, które nie zmieniają się po transpozycji (tj. po zamianie kolumn na wiersze). Mamy krakowiany górno- i dolno-trójkątne (z zerami poniżej lub powyżej przekątnej). W wymiarze 3 na 3 wygląda to tak:

Rozważamy też krakowiany przekątne...

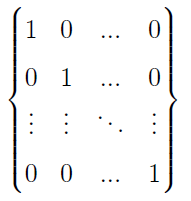
...i jednostkowe:

Te ostatnie określa się literą τ. Otóż lewostronne przemnożenie krakowianu przez taki właśnie τ jest równoważne transpozycji (co łatwo można sobie sprawdzić na prostym przykładzie; ogólny dowód też nie jest trudny).

Rozważa się także krakowian b odwrotny do danego a, tj. taki b, że ab = τ. Naturalnie tyczy się to tylko krakowianów kwadratowych. Taki b nazywamy inwersem i oznaczamy jako a^-1.

Można również zdefiniować dzielenie krakowianów. Mianowicie ilorazem krakowianów a i b nazywamy krakowian x taki, że:

Zauważmy, że dzielnik b jest w zasadzie wymiarów n x p, ale po przemnożeniu przez tau dostajemy, z uwagi na transpozycję, p x n. To, co widzimy w drugiej linijce, to w zasadzie inny zapis pierwszej. Narzuca się oczywiście analogia z normalnym dzieleniem liczb. Trzeba jednak wiedzieć, że odpowiednie wymiary krakowianów nie są warunkiem wystarczającym istnienia ilorazu. To istnienie zależy też od samych elementów krakowianu.

Przy pomocy krakowianów można zapisywać w wygodny sposób układy równań. Spójrzmy na przykład:

W skrócie można to zapisać tak:

Naturalnie pożytek z samej możliwości zapisu nie byłby zbyt duży, gdyby rachunek krakowianowy nie prowadził do wygodnej procedury rozwiązania układu. Otóż prowadzi. Rzecz opiera się na twierdzeniu, które mówi, że każdy krakowian a można rozłożyć na iloczyn dwóch krakowianów elementarnych g i h:

Krakowiany elementarne to takie, że w każdym wierszu wygasa co najmniej jedna ich kolumna. To znaczy, że w każdym wierszu jest przynajmniej jedna kolumna, która poniżej tego wiersza ma same zera. Dobrym przykładem są tu wspomniane wyżej krakowiany trójkątne, jakkolwiek w ogólności krakowian elementarny nie musi być kwadratowy. Co więcej, nie musi być tak, że w dowolnym i-tym wierszu wygasa akurat i-ta kolumna.

W każdym razie jeśli wiemy, że rozkład taki jak powyżej jest możliwy (aczkolwiek nie jest on bynajmniej jednoznaczny!), to dla rozwiązania układu należy wykonać jeszcze dwa dzielenia i wynik jest taki:

Obywamy się tu bez wzorów wyznacznikowych Cramera i zarazem jest to procedura nieco odmienna od metody eliminacji Gaussa. Co więcej, jeśli g na przekątnej ma same jedynki, to okazuje się, że iloczyn wyrazów na przekątnej czynnika h będzie równy wyznacznikowi układu.

Oczywiście rodzi się pytanie o to, jak wygląda realizacja tej procedury, tj. rozkładu na czynniki elementarne i wykonywania dzielenia (krakowianów w ogóle). Trudno byłoby się w ten wątek zagłębiać, dość powiedzieć, że te obliczenia można zalgorytmizować, a dodatkowo w szczególnych przypadkach korzystać z pewnych uproszczeń. W swoim czasie entuzjaści krakowianów uważali, że ich metody są prostsze niż analogiczne metody macierzowe, acz dziś - w dobie komputerów - nie ma to aż takiego znaczenia.

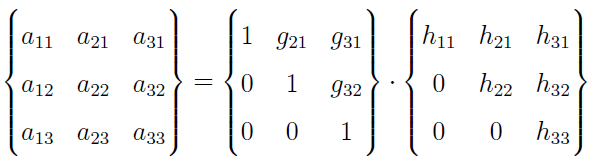
W przypadku rozkładu można założyć, że jeden z krakowianów elementarnych, np. g (przy naszych wcześniejszych oznaczeniach), ma same jedynki na głównej przekątnej. Możemy wtedy zapisać:

Zakładamy przy tym, że wielkości w krakowianie po lewej stronie równości są znane, poza tym oczywiście znamy zera i jedynki. Resztę oblicza się rekurencyjnie - zaczynając od najłatwiejszych przypadków. Na przykład z definicji mnożenia krakowianowego element a₁₁ to iloczyn pierwszej kolumny krakowianu g i pierwszej kolumny h. A więc będzie a₁₁ = h₁₁. Analogicznie h₂₁ = a₁₂. Z kolei g₂₁ = a₂₁ : h₁₁ - itd.

Poza ramy tego tekstu wykraczałaby prezentacja pełnych dowodów - np. twierdzenia o rozkładzie. Z kolei operacja dzielenia, jak wynika z podanego wyżej wzoru na x, tak naprawdę wymaga rozwiązywania układu równań liniowych - tzn. dzielenie krakowianu l przez krakowian a to rozwiązywanie układu równań o tabeli współczynników a oraz kolumnie wyrazów wolnych l. W praktyce istnieją tu rozmaite tryby i ułatwienia.

Wprowadzimy jeszcze pojęcie mnożenia wierszami, które zresztą bywa pomocne przy wykonywaniu dzielenia. Iloczyn wierszowy dwóch krakowianów a i b oznaczamy przez a w b. Rozumiemy przez to taki krakowian p', którego wyraz w i-tym wierszu i j-tej kolumnie to iloczyn i-tego wiersza a przez j-ty wiersz b. Iloczyny wierszy pojmujemy analogicznie jak iloczyny kolumn, tj. tak jak w iloczynie skalarnym, jako sumomnożenie.

Da się pokazać, że transpozycja wyniku będzie tożsama z rezultatem zwykłego mnożenia transponowanych czynników. Spójrzmy:

Wykorzystaliśmy krakowiany, które pojawiły się wcześniej, ale tym razem dokonaliśmy ich transpozycji i mnożenia wierszowego. Wynik to transpozycja pierwotnego rezultatu. Czasem jest to wygodniejsza metoda (niekoniecznie akurat przy krakowianach kwadratowych).

Dodajmy, że mnożenie krakowianowe można wyrazić przy pomocy mnożenia macierzowego. W rzeczywistości, jeśli A i B to dwie tablice liczb, wówczas A *_M B = B *_K τA. Innymi słowy, iloczyn dwóch macierzy to ich iloczyn dwóch krakowianów opartych o te same tabele, przy czym zamieniamy kolejność mnożenia, a element, który był pierwszy (a teraz jest drugi), dodatkowo transponujemy. Analogicznie przy powyższych oznaczeniach: A *_K B = B^T *_M A.

W ogólnej postaci wzór się nieco komplikuje. Można go zapisać tak: jeśli P = A₁ *_K A₂ *_K ... *_K A_n, to τP = A₁^T *_M A₂ *_M ... *_M A_n. Zauważmy, że po lewej stronie wynik krakowianowy jest transponowany.

W jednym ze starszych tekstów - przy okazji omawiana kanałów i wstęg, służących rozpoznawaniu trendów na wykresie kursu akcji - pisaliśmy o metodzie najmniejszych kwadratów. Okazuje się (o czym wspominaliśmy na początku niniejszych rozważań), że krakowiany (dzięki wprowadzeniu w nich operacji odwrotności i pierwiastka) pomogły w modyfikacji tej metody. Algorytm opracowany przez Banachiewicza okazał się szybszy i bardziej przejrzysty od klasycznego.

Krakowiany znalazły też zastosowanie w licznych zagadnieniach astronomii i geodezji (przy wyznaczaniu orbit planet) oraz mechaniki (problem dowolnej liczby obrotów ciała sztywnego wokół różnych osi). Są również wygodne w tradycyjnych zagadnieniach algebraicznych, jak schemat Hornera czy dzielenie wielomianów.

Adam Witczak

BIBLIOGRAFIA:

T. Banachiewicz, Rachunek krakowianowy z zastosowaniami, PWN Warszawa 1959

A. B. Empacher, Maszyny liczą same?, Wiedza Powszechna i Sztandar Młodych 1960

M. Gałda, Obliczenia geodezyjne i rachunek wyrównawczy, PWN 1972

T. Kochmański, Zarys rachunku krakowianowego, Główny Urząd Pomiarów Kraju, Warszawa 1948.

J. Koroński, R. Bujakiewicz-Korońska, Zastosowania matematyki w pracach naukowych Tadeusza Banachiewicza (1882 - 1954) (w pięćdziesięciolecie śmierci)

J. Kociński, Groups with involution and quasigroups with cracovian representations

J. Kociński, Cracovian algebra, Nova Science Publishers 2004

A. Strzałkowski, A. Śliżyński, Matematyczne metody opracowywania wyników pomiarów, PWN 1978

M. Tulio Rincón, Some Applications of Cracovians, Proceedings of the Meeting of the Western Region of Common, 1965.

J. T. Wędzony, Rachunek wyrównawczy dla mierniczych górniczych, Wydawnictwo Śląsk 1979