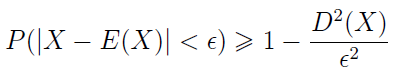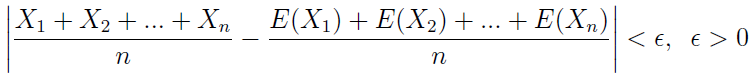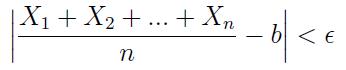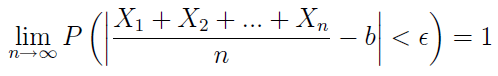Twierdzenie Czebyszewa

Załóżmy, że mamy do czynienia z pewną wielkością (np. fizyczną czy ekonomiczną), którą w pewnym sensie trudno uchwycić. Może na przykład chodzić o wielkość, która nieustannie zmienia się w czasie - być może stosunkowo nieznacznie, ale jednak; przez to w każdej sekundzie jest trochę inna. Inny casus to sytuacja, w której chcemy coś powiedzieć o wadze czy wzroście tzw. przeciętnego człowieka, przy czym teoretycznie mamy do czynienia z całą populacją, a w praktyce musimy ograniczyć się do jakiejś próby.

Temperatura ciągle się zmienia, podobnie np. kurs eurodolara. Ludzi w kraju są miliony, a na świecie miliardy, każdy ma trochę inny wzrost. Tym niemniej jakoś chcemy te wartości przybliżyć. Często postępujemy w następujący sposób: dokonujemy kilkunastu, kilkudziesięciu czy kilkuset pomiarów, po czym wyciągamy z nich średnią arytmetyczną.

Wydaje się nam naturalne, że tę właśnie średnią możemy uznać za szukaną wartość. Na tym przecież bazują sondaże przedwyborcze czy badania marketingowe wśród faktycznych i potencjalnych klientów. Próba obejmuje 500 czy 1500 osób, lecz na jej podstawie wnioskujemy o całej populacji. Podobnie rzecz się ma z wybrakowanymi produktami w fabryce: bierzemy pod uwagę jakąś próbę, np. 100 lub 1000 sztuk, choć cały wolumen produkcji jest dużo większy - i uznajemy, że odsetek uszkodzonych wyrobów jest w ogólności taki jak w rozważanej próbce.

W rzeczywistości jednak metodologia ta jest właściwa (z matematycznego punktu widzenia) tylko wtedy, gdy są spełnione pewne założenia. W praktyce zwykle są, w każdym razie wypada mieć nadzieję, że instytucje w rodzaju GUS, PBS czy CBOS dbają o to - niemniej rzecz jest istotna.

Omówimy dziś dwa pojęcia: nierówność Czebyszewa i twierdzenie Czebyszewa. To ostatnie zalicza się do tzw. praw wielkich liczb. Mówią one, ujmując rzecz ogólnie i nieformalnie, że suma dostatecznie dużej liczby zmiennych losowych niemalże zatraca losowość (przy odpowiednich założeniach). Na przykład stosunkowo łatwo możemy sobie wyobrazić, że w czterech rzutach monetą aż trzy razy wypadnie orzeł. Mimo wszystko jesteśmy w stanie to zaakceptować, przynajmniej raz. Ale gdyby w 200 rzutach aż 150 razy odnotowano orła, wtenczas mielibyśmy poczucie, że z otaczającą nas rzeczywistością dzieje się coś dziwnego. Rzeczywiście: spodziewamy się, że przy dostatecznie dużej liczbie rzutów prawdopodobieństwa orła i reszki zaczną się stabilizować przy 1/2. A przy wielu rzutach sześcienną kostką ujawni się fakt, iż każdy rezultat osiągany jest z prawdopodobieństwem 1/6.

Nie będziemy przypominać pojęć zmiennej losowej, wartości oczekiwanej czy wariancji, robiliśmy to już w poprzednich artykułach. Spójrzmy na twierdzenie, które wprowadza zapowiedzianą nierówność. 

Nierówność Czebyszewa. Prawdopodobieństwo tego, że wartość bezwzględna odchylenia zmiennej losowej X od jej wartości oczekiwanej jest mniejsza od liczby ε > 0, jest nie mniejsze niż 1 - D²(X)/ε², gdzie D²(X) to wariancja zmiennej.

W zapisie matematycznym wygląda to następująco:

Dowód niestety pomijamy, wykraczałby on poza ramy naszego tekstu. Można go znaleźć w niemal każdym podręczniku probabilistyki, przynajmniej takim, który obejmuje wstępne zagadnienia matematyki wyższej. Nasz tekst opiera się zasadniczo na publikacji W. J. Gmurmana (por. bibliografia), z niej zaczerpnęliśmy większość oznaczeń.

Sama w sobie nierówność Czebyszewa często okazuje się mało użyteczna. Wyobraźmy sobie np., że D²(X) > ε². Jest to całkiem możliwe, biorąc pod uwagę, że ε domyślnie traktujemy jako liczbę bardzo małą, w szczególności mniejszą niż 1. Wówczas otrzymujemy, że 1 - D²(X)/ε² < 0. Z nierówności Czebyszewa wynika zatem, że prawdopodobieństwa odchylenia zmiennej losowej X od jej średniej jest... nie mniejsze niż zero. To prawda, ale nie potrzeba do tego żadnej szczególnej matematyki. Rzecz wynika z samej definicji prawdopodobieństwa, które zawsze postrzegamy jako wartość nieujemną.

Nierówność Czebyszewa jest jednak wykorzystywana przy dowodzeniu twierdzenia, które ma za swego patrona tę samą osobę, czyli rosyjskiego matematyka Pafnucego Czebyszewa, żyjącego w latach 1821 - 1894.

Twierdzenie Czebyszewa. Jeśli zmienne losowe X₁, X₂, ..., X_n są parami niezależne i mają wspólnie ograniczone wariancje, to dla dowolnie małej liczby ε > 0 prawdopodobieństwo następującej nierówności:

zbliża się do jedności w miarę wzrostu liczby zmiennych, tzn.

Dowód pomijamy, pozwolimy sobie natomiast na refleksję dotyczącą przypadku szczególnego. Otóż w tezie twierdzenia dopuszcza się myśl, iż wartości oczekiwane rozważanych zmiennych losowych są różne. Ale może być i tak, że są takie same. Taką wspólną wartość oczekiwaną każdej ze zmiennych oznaczmy przez b. Wówczas twierdzenie Czebyszewa przyjmie następującą postać:

Twierdzenie Czebyszewa (przypadek szczególny). Jeśli zmienne losowe X₁, X₂, ..., X_n są parami niezależne, przy czym dla każdej zmiennej: E(X_k) = b, D²(X_k) < C, wówczas dla dowolnie małej liczby ε > 0 prawdopodobieństwo poniższej nierówności:

zbliża się do jedności w miarę wzrostu liczby zmiennych, tzn.

Co wynika z twierdzenia Czebyszewa? Na przykład to, że choć nie wiemy, jaką wartość przyjmie każda z rozpatrywanych zmiennych losowych, to jednak możemy przewidzieć, jaką wartość przyjmie ich średnia arytmetyczna. Rozproszenie poszczególnych zmiennych jest duże, ale rozproszenie ich średniej - małe. Co więcej, opisany przed chwilą przypadek szczególny pozwala twierdzić, że przy dostatecznie dużej liczbie pomiarów średnia arytmetyczna ich wyników z dużym prawdopodobieństwem różni się bardzo mało od rzeczywistej wartości mierzonej wielkości. Wynika to z faktu, że wartość ta z założenia jest równa wspólnej wartości oczekiwanej każdego wyniku (każdej ze zmiennych), tj. liczbie b.

Adam Witczak

BIBLIOGRAFIA:

W. J. Gmurman, "Rachunek prawdopodobieństwa i statystyka matematyczna", Wydawnictwa Naukowo-Techniczne 1975.

J. Jakubowski, R. Sztencel, "Rachunek prawdopodobieństwa dla (prawie) każdego", SCRIPT 2006.

"Problemy rachunku prawdopodobieństwa", praca zbiorowa, PWN 1966.