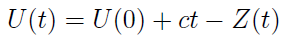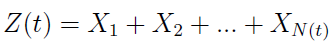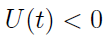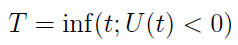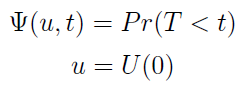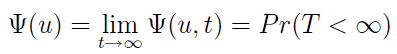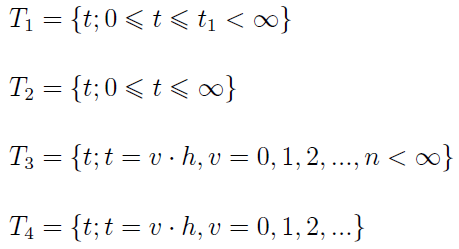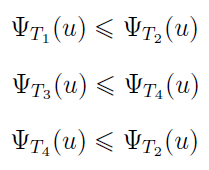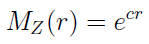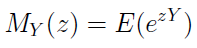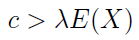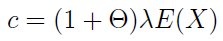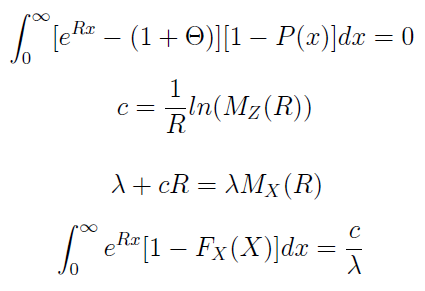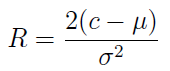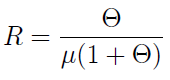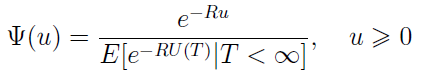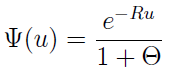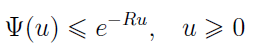Teoria ruiny

W matematyce aktuarialnej (ubezpieczeniowej) modeluje się i bada kilka głównych zagadnień. Najważniejsze tematy to: obliczanie prawdopodobieństwa zajścia szkody; - kalkulacja składki; - reasekuracja; - franszyza; - czas trwania życia osoby ubezpieczonej; - kalkulacja rezerw; - rozkład wartości indywidualnej szkody (roszczenia); - teoria ruiny.

Dziś zajmiemy się tym ostatnim zagadnieniem. Oczywiście wszystkie one są ze sobą powiązane, ale uwzględnienie możliwych zależności przekraczałoby ramy takiego artykułu.

Teoria ruiny analizuje możliwe sytuacje, w których stan kapitału firmy ubezpieczeniowej schodzi poniżej zera, przez co zaczyna brakować środków na wypłatę odszkodowań. Należy to jednak trochę doprecyzować. Najczęściej bada się prawdopodobieństwo ruiny dla konkretnego portfela, przez co tak pojęta ruina nie powinna być utożsamiana z bankructwem całego zakładu. Prawdopodobieństwo ruiny całego portfela zakładu nie musi być równe sumie prawdopodobieństw ruiny wszystkich portfeli składowych. Co więcej, zakład może oczywiście ratować się przed bankructwem (pojętym prawno-ekonomicznie) przy pomocy rozmaitych środków, takich jak np. podwyższenie stopy składki, eliminacja prób wyłudzania odszkodowań, optymalizacja umów reasekuracyjnych, wstrzymanie wypłaty dywidendy (o ile jest wypłacana), czy wreszcie pozyskanie zewnętrznych źródeł finansowania (kredyty i pożyczki, inwestorzy strategiczni).

Przejdźmy do kwestii matematycznych, nie troskając się już o to, czy mówimy o jednym z wielu portfeli czy też o portfelu sumarycznym. Mamy po prostu pewien zasób środków finansowych, oznaczony symbolem U(t). Jest on zależny od czasu (czyli od zmiennej t). Napływ składek jest stały w czasie. Spójrzmy na poniższy wzór:

Formuła ta opisuje stan środków pieniężnych w momencie t. U(0) to oczywiście kapitał początkowy, natomiast Z(t) definiujemy tak:

Jest to suma wartości szkód, które wystąpiły do momentu t, przy czym N(t) to po prostu liczba szkód. Należy mieć na uwadze, że ta liczba, podobnie jak wysokość każdej szkody, to zmienna losowa (modelowana pewnym rozkładem). W tym sensie cechą Z(t) jest podwójna losowość.

I jeszcze jeden niuans: w miejsce ct moglibyśmy wpisać P(t), tzn. przyjąć, że tempo napływu składek nie jest stałe tylko w jakiś sposób zmienne, zależne od czasu. Zajmujemy się jednak modelem uproszczonym.

Interesuje nas sytuacja, w której kapitał zejdzie poniżej zera:

Sytuacja ta nastąpić może w niektórych momentach, nas ciekawi przede wszystkim pierwsza z takich chwil:

Przez 'inf' rozumiemy infimum - kres dolny momentów t.

A tak pojmujemy prawdopodobieństwo ruiny w czasie (0; t):

Prawdopodobieństwo to zależy zarówno od długości odcinka czasu, jak i od początkowej puli pieniędzy.

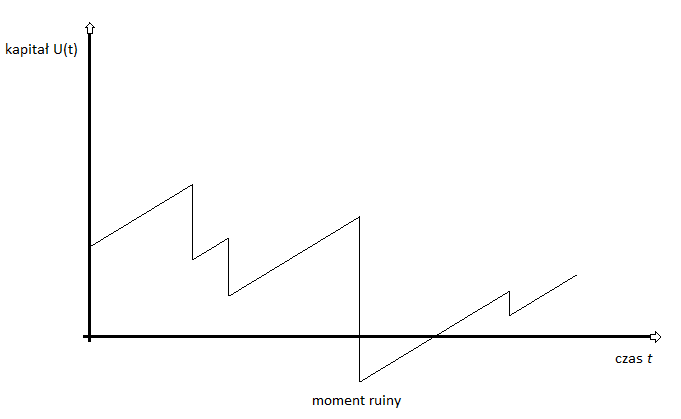
Proces zmian stanu środków może w konkretnej realizacji wyglądać np. tak:

Jak widać, w niektórych momentach wykres schodzi w dół (następuje wypłata odszkodowania), po czym znów zaczyna piąć się w górę (klienci wpłacają składki, pula środków systematycznie rośnie). W pewnym momencie U(t) schodzi jednak poniżej zera - i to właśnie jest ruina. W tej akurat realizacji udaje się w końcu ów przykry stan zażegnać.

Można rozważać również prawdopodobieństwo tego, że ruina nastąpi kiedykolwiek, tj. szansę w nieskończonym horyzoncie czasowym:

Czas możemy pojmować jako zmienną ciągłą lub dyskretną, co daje nam cztery możliwości określenia zbioru T (w zależności od tego, czy jest on skończony, czy też nie):

Moża wykazać (dość łatwo czy wręcz intuicyjnie) zachodzenie następujących zależności:

Kluczowe jest jednak pytanie o to, jak obliczyć prawdopodobieństwo ruiny. Trzy zasadnicze metody, a właściwie grupy metod, to podejścia: analityczne, aproksymacyjne i symulacyjne. My zajmiemy się głównie pierwszym z nich, a drugim jedynie marginalnie (pomijając trzecie). Interesować będzie nas model z czasem ciągłym.

Otóż oblicza się tzw. współczynnik dopasowania. Jest to dodatnie rozwiązanie równania o następującej postaci:

Po lewej stronie mamy funkcję tworzącą momenty rozkładu sumy odszkodowań. Ta z kolei jest definiowana jako następująca wartość oczekiwana:

Przez Y rozumiemy zmienną losową. W naszym przypadku opisuje ona sumę odszkodowań i będziemy oznaczać ją literą X. Więcej o funkcjach tworzących momenty znaleźć można w dowolnym podręczniku do rachunku prawdopodobieństwa, przynajmniej dla szkół wyższych.

Za parę chwil zobaczymy, do czego przydaje się współczynnik dopasowania - na razie bowiem wydaje się być wzięty ad hoc, bez wyraźnego powodu. Nawiasem mówiąc, W. Ronka-Chmielowiec wprost pisze, że "współczynnik dopasowania właściwie nie ma prostej, jednoznacznej interpretacji".

W każdym razie obliczenie tego współczynnika (oznaczanego zwykle literą R) na ogół nie jest rzeczą prostą. Pewnym ułatwieniem jest przyjęcie następujących założeń:

1) Proces występowania szkód jest jednorodnym procesem Poissona z parametrem λ. Innymi słowy, taki właśnie jest proces zliczający N(t), tzn. według procesu Poissona układają się momenty szkód (roszczeń).

Rozważa się oczywiście i inne modele, np. takie, w których proces zliczający jest określony złożonym rozkładem dwumianowym. My to pomijamy.

2) Zachodzi następująca zależność:

Oznacza to, że napływ składki w badanym okresie przewyższa oczekiwaną sumę szkód. Pominięcie tego założenia byłoby w pewnym sensie wygodne, ale mało produktywne: wówczas bowiem prawdopodobieństwo wystąpienia ruiny wyniosłoby 1, a współczynnik dopasowania w ogóle by nie istniał.

Tutaj mała uwaga: w niektórych momentach prezentujemy pewne wzory, zależności i twierdzenia. Otóż na ogół nie będziemy ich dowodzić. Odpowiednie wyprowadzenia bywają długie i rozbiłyby tok wywodu, niepotrzebnie go gmatwając. Bardziej dociekliwy czytelnik powinien mieć to na uwadze (zawsze może też sięgnąć do bibliografii).

Zakładamy, że składka c wyznaczana jest zgodnie z tzw. zasadą wartości oczekiwanej. Z tego powodu obrazuje ją następujący wzór:

Przez θ rozumiemy tzw. narzut bezpieczeństwa. Nie jest to jedyny sposób kalkulacji składki, inne typowe metody to np. zasady odchylenia standardowego, wariancji i wartości oczekiwanej funkcji, a także zasada wykładnicza. Nie będziemy jednak rozwijać tej dygresji.

Przy poczynionych założeniach okazuje się, że współczynnik R można wyprowadzić z następujących (równoważnych sobie) równań:

Jeżeli zmienna losowa opisująca wysokość łącznej szkody Z ma rozkład normalny z wartości oczekiwaną  μ i odchyleniem standardowym σ, to współczynnik dopasowania można opisać następującym wzorem:

Jeżeli natomiast o rozkładzie pojedynczej szkody (podkreślmy, pojedynczej) wiemy, że jest on wykładniczy, to wtedy prawdziwy jest następujący wzór:

Przez μ rozumiemy parametr rozkładu wykładniczego, jest to zresztą po prostu wartość oczekiwana zmiennej losowej.

Powróćmy do naszych dwóch głównych założeń (o tym, że szkody pojawiają się w zgodzie z procesem Poissona oraz że przypływ składki jest większy niż oczekiwana suma szkód). Otóż jeżeli te założenia są spełnione, to wówczas prawdziwa jest następująca formuła:

Teraz już widzimy, do czego przydaje się współczynnik dopasowania. Wyprowadzenie wzoru oczywiście pomijamy, niemniej widać, że jeśli obliczymy R na podstawie dostępnych danych (kapitał początkowy u i czas T są znane), to umożliwi nam to obliczenie prawdopodobieństwa ruiny.

Jeżeli wysokość pojedynczej szkody ma rozkład wykładniczy, to powyższa formuła może zostać przekształcona do następującej postaci:

Ogólnie jednak sprawa jest znacznie bardziej skomplikowana, w szczególności trudne jest wyliczenie mianownika formuły. Wówczas można zastosować tzw. nierówność Lundberga - cały czas pamiętając o założeniach 1) i 2).

Zawsze coś, aczkolwiek nierówność ta przeszacowuje prawdopodobieństwo ruiny, niekiedy nawet kilka razy w stosunku do faktycznego.

Oczywiście istnieją lepsze (dokładniejsze) oszacowania, ale wymagają one dodatkowych założeń lub też bardziej zaawansowanych obliczeń. Możliwe jest także szacowanie prawdopodobieństwa ruiny w modelach z czasem dyskretnym. Bada się również związki prawdopodobieństwa ruiny z takimi reasekuracją oraz z obliczaniem składki. W tym ostatnim przypadku chodzi o to, by ustalić wysokość składki przy znanym prawdopodobieństwie ruiny. Rodzą się wówczas dodatkowe pytania (i odpowiedzi) - na przykład o to, jak uwzględnić dywidendy wypłacane inwestorom albo jaki przyjąć kapitał początkowy, by móc zminimalizować składkę (tak, aby zakład był konkurencyjny wobec innych).

Adam Witczak

BIBLIOGRAFIA:

W. Ostasiewicz, Podstawowe problemy teorii ruiny, w: Metody matematyczne, ekonometryczne i informatyczne w finansach i ubezpieczeniach, część 1, praca zbiorowa, red. P. Chrzan, Wyd. Akademii Ekonomicznej w Katowicach 2006.

W. Ronka-Chmielowiec, Problem wypłacalności zakładów ubezpieczeń a prawdopodobieństwo ruiny, w: Metody matematyczne, ekonometryczne i informatyczne w finansach i ubezpieczeniach, część 1, praca zbiorowa, red. P. Chrzan, Wyd. Akademii Ekonomicznej w Katowicach 2006.

P. Kowalczyk, E. Poprawska, W. Ronka-Chmielowiec, Metody aktuarialne, PWN 2013.

B. Błaszczyszyn, T. Rolski, Podstawy matematyki ubezpieczeń na życie, WNT 2004

R. Szekli, Matematyka ubezpieczeń majątkowych i osobowych, skrypt (Uniwersytet Wrocławski).

R. Szekli, Teoria ryzyka, skrypt (Uniwersytet Wrocławski).

W. Otto, Ubezpieczenia majątkowe, WNT 2004.