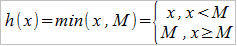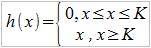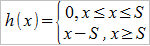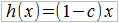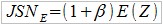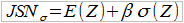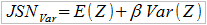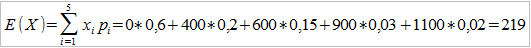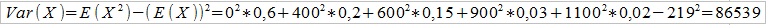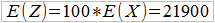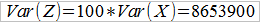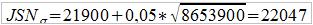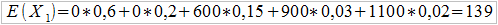Franszyza w ubezpieczeniach majątkowych

Zakłady ubezpieczeniowe starają się ograniczać koszty wynikające z likwidacji szkód poniesionych przez swoich klientów, jak również możliwie zmniejszać wielkość ponoszonego ryzyka. Z jednej strony firmy chronią się przed wypłatą odszkodowań nadmiernej wysokości (i w tym celu ustalają górną granicę vel górny limit odpowiedzialności), z drugiej natomiast – nieco paradoksalnie – nie chcą wypłacać kwot zbyt małych.

Ta druga kwestia ma swoje źródło w tym, że takich kwot – powstających z niewielkich szkód – mogłoby być bardzo dużo, co już samo w sobie byłoby niepokojące, a jednocześnie niosłyby one z sobą zbyt wysokie koszty manipulacyjne.

Nawiasem mówiąc, także i klienci godzą się na pewne ograniczenia odpowiedzialności zakładu, ponieważ dzięki temu mogą płacić niższą składkę. Towarzystwo mniej pobiera i mniej daje, tym niemniej rekompensuje taką część szkody, jaka satysfakcjonuje ubezpieczonego. Taka w każdym razie jest teoria.

Częściowe ubezpieczenie, ograniczanie swej odpowiedzialności przez zakład – to także czynniki, które ogólnie mają zachęcić klientów do rozsądnego postępowania, tj. do tego, by nie angażować się pochopnie w sytuacje obarczone ryzykiem.

Jeśli chodzi o górny limit odpowiedzialności, to sprawa wygląda tak: zakład pokrywa całość szkody, jeżeli nie przekroczy ona pewnej ustalonej kwoty M. Jeżeli szkoda będzie większa od limitu, wówczas ubezpieczony musi radzić sobie sam.

Funkcję wypłaty określamy jako h(x), gdzie x to wysokość szkody. M to, jak wspomnieliśmy, limit. Naturalny jest więc wzór:

Wysokość odszkodowania wypłacanego przez zakład jest więc od pewnego momentu stała. Jeśli chodzi o zagadnienie drobnych szkód, to w tym wypadku stosuje się technikę franszyzy. Dwa jej zasadnicze rodzaje to: 1) franszyza integralna; 2) franszyza redukcyjna. W pierwszym przypadku założenie jest takie, że do pewnej wysokości szkoda w ogóle nie jest pokrywana, natomiast odszkodowanie – i to w pełnej kwocie (chyba że gdzieś "wyżej" mamy jeszcze bonusowo górny limit, ale ten casus tu pomijamy) wypłacane jest wtedy, gdy szkoda przekroczy kwotę. Minimalną konieczną wysokość szkody oznaczmy przez K. Funkcja wypłaty wygląda więc tak:

Drugie podejście do problemu małych szkód, to franszyza redukcyjna. Ma ona dwie odmiany: 1) kwotową, w której odszkodowanie obniżane jest o stałą, określoną sumę – oraz 2) proporcjonalną, gdzie odszkodowanie pomniejszane jest o pewien procent. W przypadku kwotowym wzór wygląda następująco:

Jak widać, do pewnej kwoty S zakład nie płaci nic, a następnie obniża za każdym razem odszkodowanie o tę właśnie liczbę S. W ujęciu proporcjonalnym ustalamy wpierw współczynnik c z przedziału (0; 1), po czym wzór funkcji wypłaty okazuje się nader prosty:

Wypada przetestować przedstawione modele postępowania, przynajmniej niektóre. Zrobimy to oczywiście przy użyciu zupełnie przykładowych danych. Wpierw jednak przypomnimy trzy poznane wcześniej wzory na składkę. Są to metody: wartości oczekiwanej (zmiennej Z, opisującej wysokość odszkodowania w portfelu), odchylenia standardowego i wariancji.

Obliczeń dokonamy dla dwóch pierwszych modeli. Grecką literą β oznaczyliśmy narzut bezpieczeństwa, przy czym formalnie wypadałoby przy każdej ze składek użyć innego oznaczenia (np. α, γ), ale założymy tu, że w każdej wersji użyjemy takiego samego narzutu, niech będzie to β = 5%. Oto rozkład wysokości szkód w naszym ubezpieczeniu:

Oznacza to, że np. z 60-procentowym prawdopodobieństwem "nic się nie stanie", nie zaistnieje szkoda, tzn. żadna jej potencjalna wartość. Na 20% oceniono szansę, że szkoda będzie opiewać na 400 zł, natomiast prawdopodobieństwo, że będzie to aż 1100 zł – jest bardzo małe, wynosi 2%. Załóżmy, że nasz zakład posiada 100 takich polis, czyli mamy 100 klientów, w przypadku których można tak opisać sytuację. Obliczymy najpierw wartość oczekiwaną pojedynczej szkody, następnie jej wariancję, a później analogiczne wartości dla całego portfela, by móc skorzystać z podanych wyżej wzorów. Na razie zakładamy brak jakiejkolwiek franszyzy.

Przy obliczaniu wariancji skorzystamy ze znanego wzoru:

Pamiętamy, że mamy 100 takich polis. Czyli:

W tej sytuacji mamy (przy, jak założyliśmy, 5-procentowym narzucie bezpieczeństwa):

To oczywiście zbiorcze składki dla całego portfela (drugi wynik jest zresztą przybliżony), każdą z nich należy teraz podzielić przez 100, by otrzymać składki dla pojedynczego klienta. Wyniki to 229,95 oraz 220,47. Można wyobrażać sobie, że chodzi o kwoty w złotówkach, zapis ten pomijamy.

A teraz dokonamy modyfikacji, uzbrojeni w wiedzę o franszyzie. Zastosujemy franszyzę integralną z limitem na 400 zł. Co to oznacza? Cóż, można rzec, iż zakres zerowego prawdopodobieństwa szkody poszerzy się o sytuacje, w których szkoda ta opiewa na kwotę mniejszą lub równą od 400. Oczywiście wypadki mogą zajść, ale nie będą interesowały zakładu. Będziemy więc posługiwać się nową zmienną losową do opisu wysokości odszkodowania, oznaczymy ją przez X₁. Natomiast Z pozostaje takie samo. Wtedy:

Var(X₁) będzie równe 83179. A zatem E(Z) = 13900, Var(Z) = 8317900. Składki JSN_E oraz JSN_σ wyniosą w takim układzie 14595 zł oraz 14044,2, czyli pojedyncze będą równe 145,95 oraz 140,44.

A teraz wykonajmy obliczenia dla franszyzy procentowej, w której każde odszkodowanie jest pomniejszane o 15% wartości szkody (to podejście jest w praktyce częściej spotykane niż ryczałt). W takim układzie można przyjąć, że wysokość pojedynczego odszkodowania opisuje nowa zmienna losowa postaci X₂ = 0,85*X.

Wówczas E(X₂) = 0,85*E(X) = 0,85*219 = 186,15. Dalej: Var(X₂) = 0,852*Var(X) = 62524,4 (wynik przybliżony). Korzystamy tu z zależności znanych w rachunku prawdopodobieństwa. E(Z) = 100*E(X₂) = 18615, Var(Z) = 100*Var(X₂) = 6252440. W rezultacie składki wartości oczekiwanej i odchylenia standardowego będą równe odpowiednio 19545,75 (na osobę 195,45) oraz 18740 (na osobę 187,4).

Naturalnie nie należy sądzić, że zastosowane dane odpowiadają jakimkolwiek praktycznym przypadkom z faktycznie działających zakładów ubezpieczeń. Również i prosty rozkład prawdopodobieństwa, jaki zastosowaliśmy, jest cokolwiek wątpliwy, podobnie jak fakt, że ograniczamy się tylko do składki netto, a nie brutto (czyli np. uwzględniającej dodatkowo koszt działania zakładu). Ogólne zasady są jednak właśnie takie, jak tu przedstawiono.

Widzimy, że franszyza pozwala obniżyć składkę – ale wynika z tego, że równocześnie nie możemy liczyć na niewielkie odszkodowanie, zatem musimy dbać bardziej o to (jako klienci), by nie eskalować ryzyka. Franszyza jest uzasadniona, ponieważ w praktyce ubezpieczeniowej rozkłady są na ogół prawoskośne, co oznacza, że zachodzi wiele szkód drobnego rozmiaru (ich częstość jest wysoka), niewiele jest natomiast szkód o wysokiej wartości.

E. Stroiński przywołuje np. dane Zarządu Głównego Straży Pożarnych, z których wynika, że w latach 1996 – 2005 małe pożary ("małe" według pewnej kwalifikacji przyjętej przez Straż Pożarną) stanowił aż 88 proc. wszystkich przypadków, średnie 11 proc., zaś duże – tylko 1 proc. W tym samym okresie, jak czytamy, wypadki śmiertelne stanowiły raptem 0,6 proc. wszystkich wypadków przy pracy, "ciężkie" 1,5 proc., pozostałe natomiast 97,9 proc. Celem stosowania franszyzy jest więc doprowadzenie do tego, by szkody, które klient może sam sobie pokryć – ale też (co do zasady) tylko te szkody – były wyłączone z ubezpieczenia.

Adam Witczak

Bibliografia:

E. Stroiński, Kombinacja zatrzymania ryzyka i ubezpieczenia, Wiadomości Ubezpieczeniowe 2/2009.

P. Kowalczyk, E. Poprawa, W. Ronka-Chmielowiec, Metody aktuarialne, PWN 2013