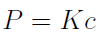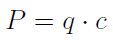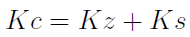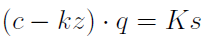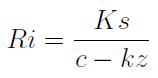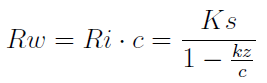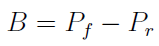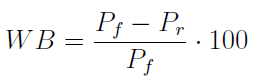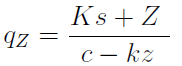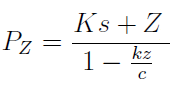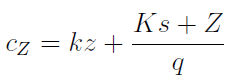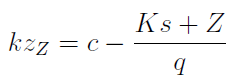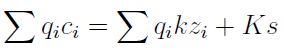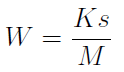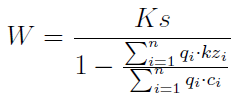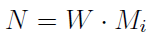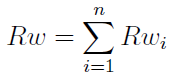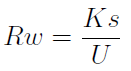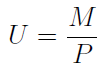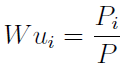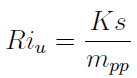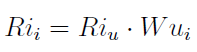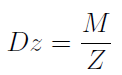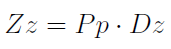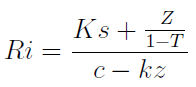Analiza progu rentowności

Progiem rentowności nazywamy taką wielkość produkcji (wolumen liczony w sztukach), przy której przychody ze sprzedaży wyrobów stają się równe kosztom całkowitym.

Ujmując rzecz ściślej, wyróżniamy ilościowy próg rentowności (zdefiniowany wyżej) i próg wartościowy. Ten ostatni to właśnie owa graniczna kwota przychodów. Jeżeli uda się ją przekroczyć, to generujemy zysk.

Naturalnie w naszej analizie przyjmiemy szereg uproszczeń. Zakładamy na przykład, że wraz ze wzrostem przychodów najpierw ograniczamy stratę (o ile ona występuje), a następnie - po przekroczeniu progu - zwiększamy zysk (teoretycznie w nieskończoność). W praktyce nie zawsze tak jest. Zdarza się nawet, że zarząd przedsiębiorstwa świadomie rezygnuje z części przychodów, by dzięki temu powiększyć rentowność zysku, a nawet jego kwotę. Rzecz polega na tym, by ograniczyć lub całkowicie wyłączyć te segmenty produkcyjne, które są mało rentowne lub wręcz przynoszą straty. Równocześnie skoncentrować można się na rozwijaniu obszarów bardziej zyskownych.

Inne uproszczenie dotyczy funkcji łączącej przychody z kosztami: zakładamy, że jest ona liniowa. W zaawansowanych rozważaniach bada się także zależności nieliniowe. Stosunek liniowy dotyczy zazwyczaj tylko krótkiego okresu. W ogóle zresztą podstawowa analiza progu rentowności ma zastosowanie krótkoterminowe, bo pomija np. zmiany w otoczeniu rynkowym, zmiany produktywności majątku i inne kwestie.

Wszystko to jednak nie zmienia faktu, że taka analiza, jaką przedstawimy, to pewien kościec, który można doskonalić i modyfikować. Przejdźmy do rzeczy. Punktem wyjścia jest dla nas poniższe równanie:

Po lewej stronie mamy P (przychody ze sprzedaży), po prawej Kc, tj. koszty całkowite. Przychody rozpisać można następująco:

Jest to iloczyn liczby sprzedanych wyrobów (q) oraz ceny pojedynczej sztuki (c).

Koszty rozbijamy następująco:

Jest to podział na (całkowite) koszty zmienne (Kz) i stałe (Ks). Podział ten nie wynika z przepisów o rachunkowości i co do zasady nie jest uwzględniany w bilansie. Tym niemniej jest on istotny - nawet jeśli musimy się zdobyć na pewną arbitralność.

Otóż koszty stałe zasadniczo nie zależą od wielkości produkcji i sprzedaży. W tej grupie są np.:

- płace zarządu
- koszty leasingu
- amortyzacja (zwłaszcza budynków fabrycznych) i czynsze
- odsetki od kredytów
- koszty badań i rozwoju

Koszty zmienne mają do siebie to, że rosną i spadają równolegle ze zmianami wielkości produkcji i sprzedaży. W naturalny sposób narzuca się tu myślenie o kosztach rosnących proporcjonalnie lub progresywnie - tj. wprost proporcjonalnie do produkcji albo szybciej od niej. Istnieją jednak także koszty degresywne (rosnące wolniej niż sprzedaż) oraz regresywne. W tym ostatnim wypadku zwiększenie produkcji prowadzi do redukcji kosztów (w praktyce zdarza się to rzadko).

Przykładem kosztu degresywnego bywa niekiedy zużycie materiałów. Mowa o sytuacji, w której firma co prawda potrzebuje więcej materiałów (bo zwiększa produkcję swoich wyrobów), ale właśnie dlatego jest w stanie zażądać od dostawców niższej ceny jednostkowej.

Przykłady kosztów zmiennych widzimy poniżej:

- koszty materiałów bezpośrednich
- koszty energii i paliw zużywanych przy produkcji
- wynagrodzenia pracowników produkcyjnych (o ile zależą od zmian wielkości produkcji)
- prowizje sprzedażowe (j.w.)

Nie wszystkie koszty da się jednoznacznie uznać za stałe lub zmienne. W takiej pośredniej grupie są np. koszty energii czy konserwacji i remontów. Wypada jednak je wtedy podzielić na część stałą i zmienną - licząc się z tym, że takie rozróżnienie może być obarczone pewnym błędem.

Całkowite koszty zmienne są iloczynem q (liczby sprzedanych produktów) i kz - tj. jednostkowego kosztu zmiennego. Dzięki temu nasz początkowy wzór możemy przekształcić do następującej wersji:

Po lewej stronie mamy pewien iloczyn. Jego lewy czynnik to tzw. jednostkowa marża pokrycia. Inaczej mówiąc, to całkowite koszty stałe podzielone przez liczbę sprzedanych wyrobów (wystarczy obie strony podzielić przez q - wtedy to zobaczymy).

Wykonajmy jednak inne przekształcenie: takie, które pozwoli nam uzyskać wielkość q. Oznaczymy ją jako Ri.

Po lewej stronie mamy teraz ilościowy próg rentowności. Właśnie tyle sztuk potrzeba, by przychody z ich sprzedaży zrównoważyły koszty całkowite.

Sprawdźmy zatem, ile wyniosą te progowe przychody:

Wzór powyższy prezentuje nam tzw. wartościowy próg rentowności (Rw).

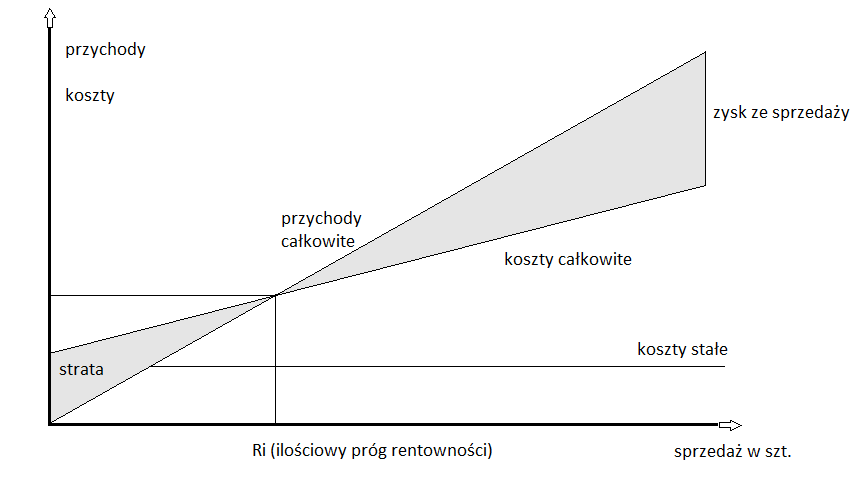
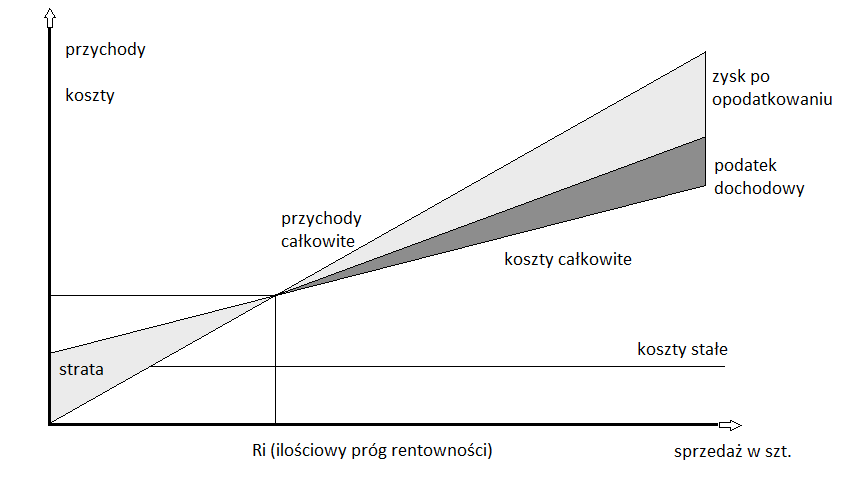
Omówione dotąd kwestie zostały zaprezentowane na poniższym wykresie:

Na osi x mamy wolumen sprzedaży w sztukach. Na osi y prezentujemy dwie wielkości zależne od tegoż wolumenu, mianowicie przychody i koszty całkowite. Dopóki sprzedaż nie jest dostatecznie duża, dopóty koszty przeważają nad przychodami - i wówczas mamy stratę. Po przejściu przez Ri przedsiębiorstwo generuje już zysk (ze sprzedaży).

Można zmierzyć różnicę pomiędzy przychodami w progu rentowności a tymi przychodami, które faktycznie osiągnęliśmy (albo tymi, które planujemy czy też chcemy wygenerować). Ta różnica (ozn. B) to tzw. strefa bezpieczeństwa:

Ta różnica to zarazem informacja o tym, jak bardzo można obniżyć wpływy ze sprzedaży, by nie zejść w obszar straty. To samo można też wyrazić procentowo przy pomocy tzw. procentowego wskaźnika bezpieczeństwa (WB):

Jeśli wiemy, jaki chcemy osiągnąć zysk oraz znamy koszty stałe, jednostkowy koszt zmienny i cenę jednej sztuki - to możemy obliczyć, ile sztuk należy wyprodukować, by zamierzony zarobek wypracować. Punktem wyjścia jest założenie, że tym razem P = Ks + Z. Tym razem nie mówimy więc o sytuacji progowej, a o nadwyżce obrotów nad kosztami.

W podobny sposób obliczamy przychody konieczne do wypracowania żądanego zysku:

Analogicznie możemy obliczyć cenę jednostkową gwarantującą (rzecz jasna ceteris paribus) oczekiwany zysk przy znanych kosztach i możliwościach produkcyjnych:

Podobnie rzecz się ma z jednostkowym kosztem zmiennym:

Przykład.

Wyobraźmy sobie, że firma wytwarza i sprzedaje tylko jeden wyrób (tj. wyrób jednego gatunku). W badanym okresie (np. rocznym) sprzedaje się 700 sztuk, cena jednostkowa to 45 zł, zaś jednostkowy koszt zmienny to 18 zł. Koszty stałe to 14.850 zł.

Zastosujmy przedstawione wcześniej wzory. Ilościowy próg rentowności to 14.850/(45 - 18) = 550 sztuk. Próg wartościowy to 14.850/(1 - 18/45) = 24.750 zł. Strefa bezpieczeństwa to 45(700 - 550) = 6750 zł. To znaczy, że jeśli aktualnie sprzedajemy 700 sztuk (po 45 zł od egzemplarza, co razem daje 31.500 zł faktycznych przychodów), to możemy zmniejszyć obrót nawet o 6750 zł, a i tak nie popadniemy w stratę.

Daje to wskaźnik bezpieczeństwa WB = 21,4 proc., który można uznać za całkiem wysoki.

Jaki mamy zysk na 700 egzemplarzach? To 31.500 - 700*18 - 14.850 = 4.050 zł. Daje to procentową marżę na sprzedaży 12,8 proc.

Produkcja wieloasortymentowa

Dotychczas rozważaliśmy bardzo prosty model przedsiębiorstwa. Zakładaliśmy mianowicie, że wytwarza ono produkt tylko jednego rodzaju. Tak naprawdę asortyment obejmuje zazwyczaj kilka lub więcej klas (zdarza się, że są ich dziesiątki).

Punktem wyjścia będzie teraz następujące równanie - opisujące równość przychodów i kosztów:

Po lewej stronie mamy przychody wyrażone jako suma iloczynów. Każdy iloczyn ma dwa czynniki: cenę jednostkową i-tego wyrobu i liczbę sprzedanych sztuk. Prawa strona to suma kosztów całkowitych i zmiennych, przy czym w zmiennych uwzględnia się zróżnicowanie asortymentu.

Pojawia się jednak pewien problem: jak rozliczyć koszty stałe? To znaczy: jak mają się one do różnych produktowych? Możliwe są trzy rozwiązania:

1) koszty stałe rozlicza się w całości na poszczególne produkty

2) koszty stałe odnosi się w całości do przedsiębiorstwa

3) podejście mieszane: część kosztów stałych odnosi się do poszczególnych klas asortymentowych, a część do całego przedsiębiorstwa.

Zajmiemy się teraz metodą pierwszą. Tutaj oddzielnie ustala się progi rentowności dla wszystkich klas wyrobów. W pierwszej kolejności obliczamy wskaźnik narzutu kosztów stałych przedsiębiorstwa:

Przez Ks rozumiemy nadal koszty stałe firmy, zaś M to całkowita marża pokrycia ze sprzedaży wszystkich produktów. Z tego powodu wzór można zapisać również w sposób następujący:

Można ustalić także narzut kosztów stałych na poszczególne grupy produktów (przez M_i rozumiemy całkowitą marżę pokrycia i-tego wyrobu):

W tej sytuacji możemy dla każdego wyrobu wykonać analizę progu rentowności (osobno). Później wyliczamy całkowity wartościowy próg rentowności:

Przykład.

Załóżmy, że mamy trzy produkty: A, B i C. W tabeli podaliśmy wolumeny ich produkcji (w sztukach), jednostkową cenę sprzedaży (CJS), jednostkowy koszt zmienny (JKS) i jednostkową marżę pokrycia (JMP). Do tego przyjmujemy koszty stałe na poziomie 34.125 zł.

Marże pokrycia dla poszczególnych produktów są następujące:

A: 500 * 35 = 17.500
B: 250 * 35 = 8.750
C: 1500 * 15 = 22.500

Zauważmy, że marże te moglibyśmy obliczyć także z innego wzoru, np. dla A byłoby to: (75 - 40) * 500. Oczywiście to jest to samo, ale drugie podejście przypomina nam, że jednostkowa marża pokrycia to różnica pomiędzy ceną sprzedaży a jednostkowym kosztem zmiennym.

Wskaźnik narzutu kosztów stałych jest taki: 34.125 / (17.500 + 8.750 + 22.500) = 34.125 / 48.750 = 0,70.

Tym samym narzuty kosztów stałych dla poszczególnych produktów wyglądają tak:

A: 17.500 * 0,7 = 12.250 zł
B: 8.750 * 0,7 = 6.125 zł
C: 22.500 * 0,7 = 15.750 zł

Jak pamiętamy, próg ilościowy rentowności to iloraz kosztów stałych oraz (jednostkowej!) marży pokrycia. Stosujemy ten wzór po kolei do każdego wyrobu:

A: 12.250 / 35 = 350 sztuk
B: 6.125 / 35 = 175 sztuk
C: 15.750 / 15 = 1050 sztuk

Progi wartościowe to w takim razie:

A: 350 * 75 = 26.250 zł
B: 175 * 90 = 15.750 zł
C: 1050 * 25 = 26.250 zł

Suma tych wartości daje nam próg całkowity: 26.250 + 15.750 + 26.250 = 68.250 zł. Powyżej takich przychodów przedsiębiorstwo będzie generować zysk. Przy naszych danych faktyczny zysk to Z = (500 * 35) + (250 * 35) + (1.500 * 15) - 34.125 = 17.500 + 8.750 + 22.500 - 34.125 = 14.625 zł.


Jeżeli przyjmujemy, że koszty stałe są w całości przypisane do przedsiębiorstwa (model nr 2), to jednoznacznie jesteśmy w stanie wyznaczyć tylko próg wartościowy. Zmieni się on, gdy zmodyfikujemy strukturę produkcji. Spójrzmy na wzór:

Próg wartościowy to iloraz kosztów stałych i wielkości U. Ta wielkość wyraża udział całkowitej marży pokrycia w przychodach ze sprzedaży:

Skoro koszty stałe są jedną wielkością, nie dzielimy ich na grupy asortymentowe, to aby ustalić ilościowy próg rentowności, musimy zastosować przeciętną jednostkową marżę pokrycia na poszczególnych produktach. W tym celu najpierw obliczamy następujące wielkości po wszystkich i:

P_i to przychody ze sprzedaży i-tego wyrobu, P to ogólna kwota obrotów. Iloraz tych wielkości daje nam Wu_i - wskaźnik udziału przychodów ze sprzedaży i-tego wyrobu w całkowitych przychodach ze sprzedaży.

Następny wzór daje nam umowny próg ilościowy:

W mianowniku mamy przeciętną jednostkową marżę pokrycia. To po prostu suma iloczynów następującej postaci: jednostka marża pokrycia i-tego wyrobu * Wu_i.

Próg ten jest wyrażony w bliżej niesprecyzowanych jednostkach umownych, a przecież trudno porównywać np. 50 zegarków i 250 broszek. Faktyczny (ale de facto też tylko przybliżony, z uwagi na użycie przeciętnej marży jednostkowej) próg ilościowy to iloczyn progu umownego oraz udziału wyrobu w przychodach:

Próg wartościowy danego wyrobu to z kolei iloczyn progu ilościowego i ceny produktu. Ostatecznie można, jak poprzednio, zsumować wszystkie progi wartościowe i trzymać próg całkowity.


Możemy jeszcze wprowadzić pojęcie dźwigni operacyjnej. Oto jej wzór:

W zasadzie to wzór na stopień dźwigni operacyjnej. Przez M rozumiemy marżę pokrycia, przez Z - zysk ze sprzedaży. Przypomnijmy, że matematycznie marża pokrycia to różnica przychodów i kosztów zmiennych, a więc to po prostu koszty stałe plus ewentualny zysk. Zachodzi następująca zależność:

Ten zapis należy rozumieć tak: Zz to procentowy wzrost zysku, zaś Pp to procentowy wzrost sprzedaży. A zatem procentowy wzrost zysku równy jest iloczynowi procentowego wzrostu sprzedaży i stopnia dźwigni (operacyjnej).  

Ostatnia rzecz to kwestia podatku. Spójrzmy na rysunek:

Ta ilustracja bierze pod uwagę to, że od zysku na sprzedaży zazwyczaj płacimy także pewien podatek dochodowy. Spójrzmy na to, jak w tej sytuacji oblicza się próg ilościowy:

Otóż ten wzór mówi nam, ile sztuk produktu należy wytworzyć, jeśli chcemy osiągnąć po opodatkowaniu planowany zysk Z przy stopie podatkowej T. Pozostałe oznaczenia są takie jak wcześniej.

Inne zagadnienia, których tu nie będziemy rozwijać, to np. analiza wrażliwości, zagadnienie minimalnego i maksymalnego progu rentowności czy planowanie wyniku w zależności od zmian struktury asortymentowej.

Adam Witczak


BIBLIOGRAFIA:

K. Czubakowska, W. Gabrusewicz, E. Nowak, Podstawy rachunkowości zarządczej, Polskie Wydawnictwo Ekonomiczne 2006.

Z. Leszczyński, T. Wnuk, Zarządzanie firmą produkcyjną za pomocą rachunkowości zarządczej i kontrolingu finansowego, Fundacja Rozwoju Rachunkowości w Polsce 1996.

M. Sierpińska, T. Jachna, Ocena przedsiębiorstwa według standardów światowych, PWN 1997.

Rachunkowość zarządcza, praca zbiorowa pod red. G. K. Świderskiej, Poltext 1997.

H. J. Vollmuth, Controlling - Instrumenty od A do Z, Agencja Wydawnicza Placet 1995.

C. Drury, Rachunek kosztów, PWN 1998.