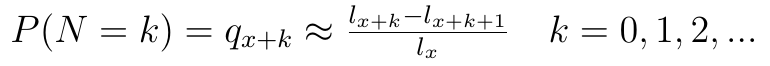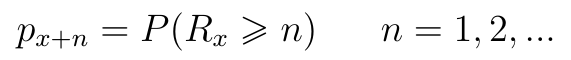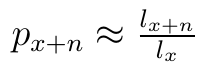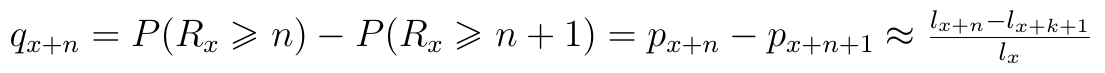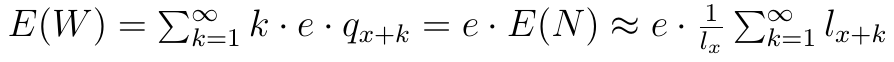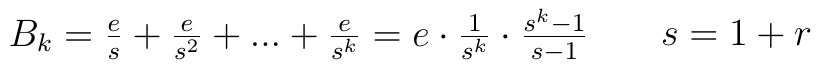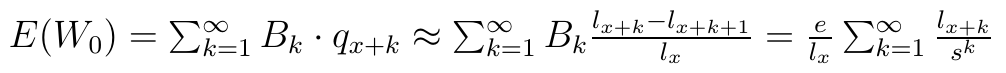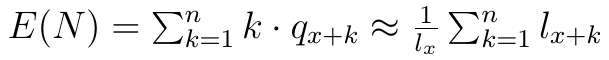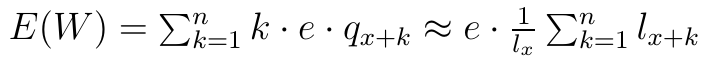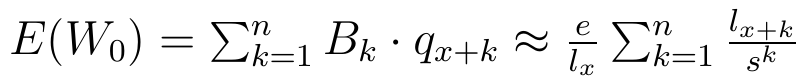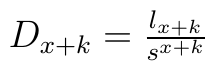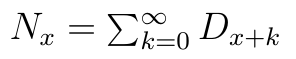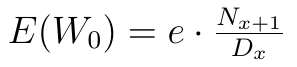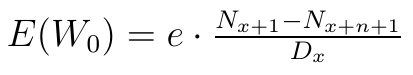Renty dożywotnie i czasowe

Renta to ciąg płatności, który dokonywany jest przez pewien czas: albo do chwili śmierci rentobiorcy, albo tylko w pewnym okresie (np. przez nie więcej niż 10 lat). Ten pierwszy rodzaj to renty dożywotnie (wieczyste), ten drugi to renty czasowe (terminowe). W każdym razie takie są dwie podstawowe kategorie podziału.

Zacznijmy od renty dożywotniej - płaconej z dołu (przypadek płatności z góry nie jest dużo bardziej złożony, niemniej pomijamy go z oszczędności miejsca). Rozważamy osobę, która ma obecnie x lat - i ma otrzymywać roczną rentę o stałej wysokości e. Jakie zagadnienia mogą nas interesować (zarówno wtedy, gdy jesteśmy rentobiorcą, jak i zakładem ubezpieczeń)?

Otóż mamy tu przynajmniej trzy wielkości losowe. Losowe, bo zależne od tego, kiedy umrze rentobiorca - a ten moment nigdy nie jest pewny. Te trzy wielkości to:

N - liczba płatności do końca życia
W - suma kwot wypłaconych do końca życia (bez reinwestowania itd.)
W₀ - wartość obecna (present value) sumy wypłaconych do końca życia kwot.

Co do zmiennej N, to rzecz jasna przyjmuje ona wartości w obrębie liczb naturalnych, począwszy od k = 0. Wskaźnik k zmierza ku nieskończoności.

Spójrzmy na poniższy wzór:

Trzeba go wyjaśnić. Liczymy prawdopodobieństwo tego, że N wyniesie k, czyli że nastąpi k wypłat, a zatem - co na jedno wychodzi - że nasz x-latek przeżyje k lat. Otóż takie prawdopodobieństwo oznacza się w matematyce aktuarialnej jako q_x+k. I rzeczywiście, takie oznaczenie zastosowaliśmy. A jak się oblicza q_x+k?

Przejdźmy na moment do wzorów ogólnych, w miejsce naszego k weźmiemy teraz n - i na chwilę zapominamy o rentach. Otóż jeśli R_x oznacza liczbę lat, które jeszcze przeżyje x-latek, to możemy obliczyć p_x+n - tj. prawdopodobieństwo tego, że x-latek przeżyje jeszcze przynajmniej n lat:

To prawdopodobieństwo szacuje się następującym ułamkiem:

Jak powinien być rozumiany ten ułamek? Skorzystaliśmy tutaj z tzw. tablic trwania życia. To tablice statystyczne, w których zapisuje się, na podstawie badań nad populacją, ilu ludzi (w populacji liczącej na początku np. 10 tys. lub 100 tys. osób) dożyło danego wieku. Innymi słowy, jeśli x to wiek, wtenczas l_x - to właśnie liczba tych, którzy dożyli (przynajmniej! - to istotne) x lat. Stąd np. x₆₀ to liczba osób, które dożyły przynajmniej 60 lat. A zatem l_x+n / l_x to stosunek liczby osób, które przeżyły co najmniej x+n lat do liczby wszystkich, którzy przeżyli przynajmniej x lat. Z kolei d_x = l_x+n - l_x+n+1 to liczba osób, które zmarły pomiędzy x+n-tym a x+n+1-szym rokiem życia. Oczywiście można też rozważać inne przedziały, gdzie w miejsce 1 podstawimy inną liczbę (i dzięki temu zbadamy np. jak wielu ludzi zmarło między 65 a 72 rokiem życia).

Wzór na p_x+n jest już jasny, rozważmy teraz q_x+n:

To jest prawdopodobieństwo, że osoba x-letnia umrze pomiędzy n-tym i n+1-szym rokiem. Na przykład, że obecny 60 lat umrze między 77 a 78 rokiem życia. Oczywiście w liczniku ułamka w ostatniej równości moglibyśmy wstawić wprowadzone wyżej oznaczenie d_x.

Wracamy do renty. Liczymy teraz rozkład zmiennej losowej W. Jeśli x-latek dożyje wieku x+k, to rentę e otrzyma k razy. Rozkład zmiennej losowej jest, jak wiemy, określany jako zbiór par postaci (x_i, p_i), gdzie x_i to wartość zmiennej, a p_i to prawdopodobieństwo osiągnięcia tejże wartości. Zatem w naszym przypadku, w przypadku zmiennej W, mamy rozkład określony parami (ek, q_x+k). Daje to następującą wartość oczekiwaną:

Obecna wartość sumy potencjalnie wypłaconych przez k lat kwot to:

Przez r rozumiemy stopę procentową (w praktyce - uśrednioną i zarazem przewidywaną). W takim razie wartość oczekiwana zmiennej W₀ to:

Ostatnia równość tak naprawdę nie jest zupełnie oczywista: i wymaga podstawień i przekształceń, dość mozolnych, choć w gruncie rzeczy prostych (dlatego je tutaj pominęliśmy). Proszę pamiętać, że e to wielkość rocznej wypłaty (a nie słynna liczba e).

Nawiasem mówiąc, to ostatnie wyrażenie w ciągu równości jest ważne. To bowiem prosty wzór na minimalną składkę netto, którą powinien uiścić obecnie przyszły odbiorca renty (np. przyszły emeryt). Składka ta jest netto - nie uwzględnia ona bowiem ani zysku towarzystwa ubezpieczeniowego, ani kosztów ponoszonych przez ubezpieczalnię w trakcie jej działalności. Że jest to składka, to rzecz zrozumiała: bo to obecna wartość przyszłej renty, a więc tyle, ile należy dziś wpłacić, by mieć przyszłą rentę. Wartość obecna, czyli zdyskontowana. A więc z wartości obecnej "uzbiera się" renta po uwzględnieniu stopy procentowej i zasady procentu składanego.

*

Teraz przejdziemy do renty czasowej. Okres ubezpieczenia to n kolejnych lat, chyba że ubezpieczony umrze szybciej. Wzory analogiczne do poprzednich będą - po wyprowadzeniu - wyglądać następująco:

Często stosuje się też następujące oznaczenia skrótowe:

Dzięki nim można nasze wzory przedstawić w uproszczonej postaci, a jest to pożyteczne, bo wielkości D_x+k i N_x są stablicowane.

Przedstawimy już tylko wzory na W₀. Dla rent dożywotnich wygląda to tak:

Dla rent czasowych mamy natomiast:

Są to wszystko bardzo podstawowe formuły. Na ich podstawie budowana jest cała, znacznie bardziej rozbudowana, teoria rent i ubezpieczeń. Rozważa się nie tylko przypadki dyskretne (o przeliczalnej lub skończonej liczbie wypłat), lecz i ciągłe (choć to raczej modele teoretyczne).

Adam Witczak

BIBLIOGRAFIA:

M. Dobija, E. Smaga, "Podstawy matematyki finansowej i ubezpieczeniowej", PWN 1995.

P. Kowalczyk, E. Poprawska, W. Ronka-Chmielowiec, "Metody aktuarialne", PWN 2013.