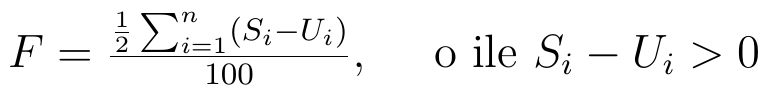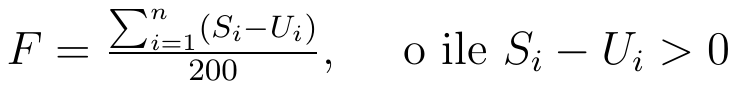Wskaźnik lokalizacji Florence'a

Istnieją państwa, w których pewne zjawiska - takie jak bezrobocie, ubóstwo czy odsetek ludności należącej do jakiejś mniejszości religijnej lub etnicznej - są mocno zróżnicowane. Na przykład w niektórych regionach kraju stopa bezrobocia jest bardzo niska (rzędu 3 - 4 proc.), w innych - bardzo wysoka (powiedzmy, że 20-procentowa, albo i wyższa). Albo też: w niektórych województwach, stanach czy departamentach prawie nie ma chrześcijan (czy np. ludności czarnoskórej), zaś w innych ludność taka jest wyraźnie obecna, a nawet dominuje.

Z drugiej strony, zjawiska tego rodzaju mogą być też rozłożone równomiernie: co wygląda np. tak, że w każdym stanie jest ok. 10 proc. muzułmanów. Albo też, że w każdym województwie jest mniej więcej tyle samo sklepów czy lekarzy na 1000 mieszkańcow.

Jak mierzyć koncentrację i rozproszenie? Można to robić rozmaicie, ale często używa się wskaźnika lokalizacji Florence'a. Został on wprowadzony w roku 1929 przez P. S. Florence'a w pracy "The Statistical Method in Economics and Political Science". Z angielskiego to "Florence's location quotient". Nie będziemy tu wnikać w szczegółowe uzasadnienie wzoru. W dodatku posługiwać się będziemy tylko jednym jego wariantem, choć narzędzie to - jak to zwykle bywa w statystyce - ma przynajmniej kilka odmian.

Wyobraźmy sobie, że na danym obszarze mamy dwie zbiorowości, które (prawdopodobnie) są ze sobą w jakiś sposób powiązane. Na przykład rozważamy województwo, a w nim - liczbę mieszkańców i liczbę sklepów. Albo: państwo Unii Europejskiej i liczbę bezrobotnych. Teraz przyjmijmy, że rozważamy pewną liczbę takich obszarów: wszystkie województwa w Polsce lub wszystkie kraje UE. Chcemy stwierdzić, czy sklepy są w Polsce rozmieszczone równomiernie; albo też czy bezrobotni są równomiernie rozmieszczeni na terenie UE.

Otóż wskaźnik (współczynnik) Florence'a liczy się następująco:

Innymi słowy:

Wyjaśnijmy użyte oznaczenia:

S_i - procentowa struktura pierwszego zjawiska
U_i - procentowa struktura drugiego zjawiska
n - liczba jednostek (obszarów), w praktyce: liczba tych obszarów, na których różnica S_i - U_i jest dodatnia.

Co to znaczy "procentowa struktura"? Zobaczmy to na przykładzie, korzystając z danych GUS za rok 2018:

Główny Urząd Statystyczny wyróżnia w Polsce 7 makroregionów: Południowy, Północno-Zachodni, Południowo-Zachodni, Północny, Centralny, Wschodni i Województwo Mazowieckie (jako odrębny region). Każdy makroregion składa się z 2 lub 3 regionów (na ogół województw, choć na Mazowszu wyróżnia się region warszawski stołeczny i mazowiecki regionalny), ale nie jest to dla nas w tej chwili istotne.

W tabeli widzimy liczbę mieszkańców każdego makroregionu, a także liczbę osób pracujących, bezrobotnych i nieaktywnych (biernych zawodowo). Liczby te są podane w tysiącach, czyli np. 3061 to w rzeczywistości 3061000, tj. 3 mln 61 tys.

Jak rozumieć L_i, P_i, B_i? Otoż wartości L_i mówią nam, jakim procentem całej ludności Polski jest ludność i-tego makroregionu. Na przykład dla Południa mamy: 6330 / 30596 = 0,2069 (w przybliżeniu), czyli 20,69 proc. Analogicznie interpretowane są P_i, B_i oraz N_i: mówią nam one, jak duża część wszystkich pracujących, bezrobotnych czy biernych w Polsce mieszka w danym makroregionie. Proszę to dobrze zrozumieć: nie chodzi o to, jaki procent mieszkańców makroregionu stanowią bezrobotni czy nieaktywni! Stąd np. wartość P_2 = 16,56 proc. to efekt następującego przeliczenia: 2720 / 16422, a nie 2720 / 4959.

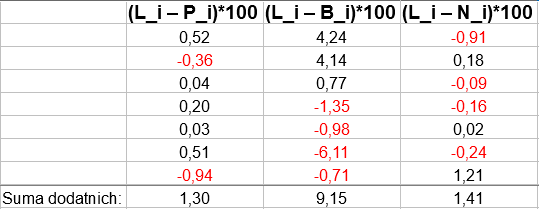
Spójrzmy na drugą tabelkę, która ma charakter pomocniczy:

Pierwotnie we wzorze Florence'a użyliśmy oznaczeń S_i oraz U_i. Teraz naszym S_i będzie we wszystkich trzech przypadkach L_i, natomiast za U_i będziemy podstawiać kolejno P_i, B_i oraz N_i. Innymi słowy, obliczymy współczynniki dotyczące tych trzech typów ludności, a więc sprawdzimy, jak duże jest rozproszenie pracujących, bezrobotnych i biernych w Polsce.

Przypomnijmy, że w tej wersji formuły, z której korzystamy, używa się jedynie dodatnich różnic S_i - U_i. Stąd np. w drugiej kolumnie tabeli pomocniczej suma wyrażeń (L_i - P_i)*100 po indeksach i to de facto suma: 0,52 + 0,04 + 0,20 + 0,03 + 0,51. Pozostałe dwa wyrażenia (-0,36 oraz -0,94) - pomijamy.

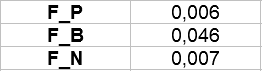
Przeliczmy trzy wskaźniki:

Wyszły nam liczby: F_P = 0,006; F_B = 0,046; F_N = 0,007 (pkt). Żeby je zrozumieć, trzeba posłużyć się jakąś zwyczajową interpretacją wskaźnika F, najlepiej tą, która jest przyjmowana standardowo. A mówi ona, że wartość F:

- w zakresie (0,0 - 0,25) oznacza wysokie rozproszenie / małą koncentrację

- w zakresie (0,25 - 0,49) oznacza średnie rozproszenie i średnią koncentrację

- w zakresie (0,49 - 1,0) oznacza niskie rozproszenie i wysoką koncentrację.

Nasze wartości są bardzo bliskie zera. Oznacza to więc, że badane zjawiska są na terenie Polski i w odniesieniu do makroregionów bardzo rozproszone. Można powiedzieć, że są rozłożone równomiernie. Nie jest np. tak, że bezrobotni (czy pracujący) są skoncentrowani w jakimś jednym czy dwóch regionach, a prawie nie ma ich w pozostałych.

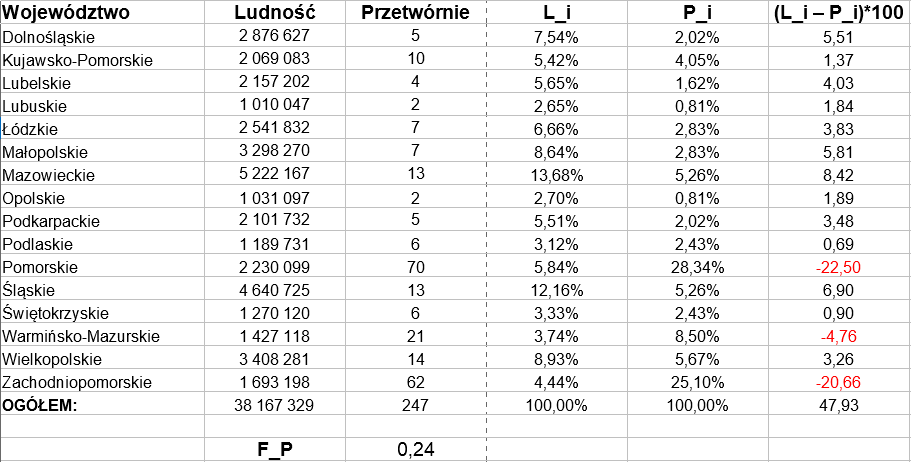
Zastosujmy teraz inne dane. Rozważmy województwa w Polsce, ich liczbę ludności (w roku 2010) oraz liczbę przetwórni rybnych w każdym województwie:

Jak łatwo zauważyć, najwięcej przetwórni rybnych jest na Pomorzu (łącznie 132 w dwóch województwach, gdy w całej Polsce takich zakładów jest 247, albo też było ich tyle przed kilkoma laty), dość dużo także na Warmii i Mazurach, w pozostałych województwach jest ich dużo mniej, zwykle po kilka. Ktoś, kto mieszka na Pomorzu, ma w pewnym sensie łatwiejszy dostęp do takich przetwórni. Na Opolszczyźnie są tylko 2 do wyboru, acz już na Górnym Śląsku aż 13.

Z obliczeń wynika, że współczynnik lokalizacji wynosi 0,24 pkt. Owszem, to wciąż znak wysokiego rozproszenia, ale jednak w porównaniu z poprzednimi wartościami, bliskimi zeru, różnica jest uderzająca. Wskaźnik prawie wchodzi w strefę średnią.

Dla porównania, wskaźnik Florence'a dla województw, obliczony pod kątem liczby hurtowni roślin ozdobnych, wyniósł w 2002 roku 0,15 pkt, zaś w 2012 był na poziomie 0,13 pkt. Tak więc rozproszenie takich hurtowni jest duże, są one rozłożone równomiernie (por. Olewnicki et al. 2015).

Z drugiej strony, inaczej ma się sprawa z przedsiębiorstwami przetwórstwa zielarskiego, analizowanymi w pracy Olewnicki et al. 2014). Tam w roku 2009 wskaźnik F wyniósł 0,786 pkt, zaś w 2012 było to 0,753 pkt. Istotnie: dla przykładu, aż 27,8 proc. firm produkujących olejki eteryczne (5 spośród 18 badanych przez GUS w 2013) mieściło się w województwie wielkopolskim, 22,2 proc. w mazowieckim, 16,7 proc. w śląskim.

Ale uwaga: we wspomnianej pracy na temat zielarstwa wskaźnik F nie był liczony w odniesieniu do liczby ludności w województwach, lecz w relacji do liczby gospodarstw zielarskich stanowiących bazę surowcową dla firm przetwarzających zioła. Tymczasem w przypadku hurtowni roślin ozdobnych odnoszono się do populacji, podobnie jak i my uczyniliśmy z przetwórniami rybnymi. Dane te nie są więc w pełni ze sobą porównywalne. Takie niuanse trzeba uwzględniać.

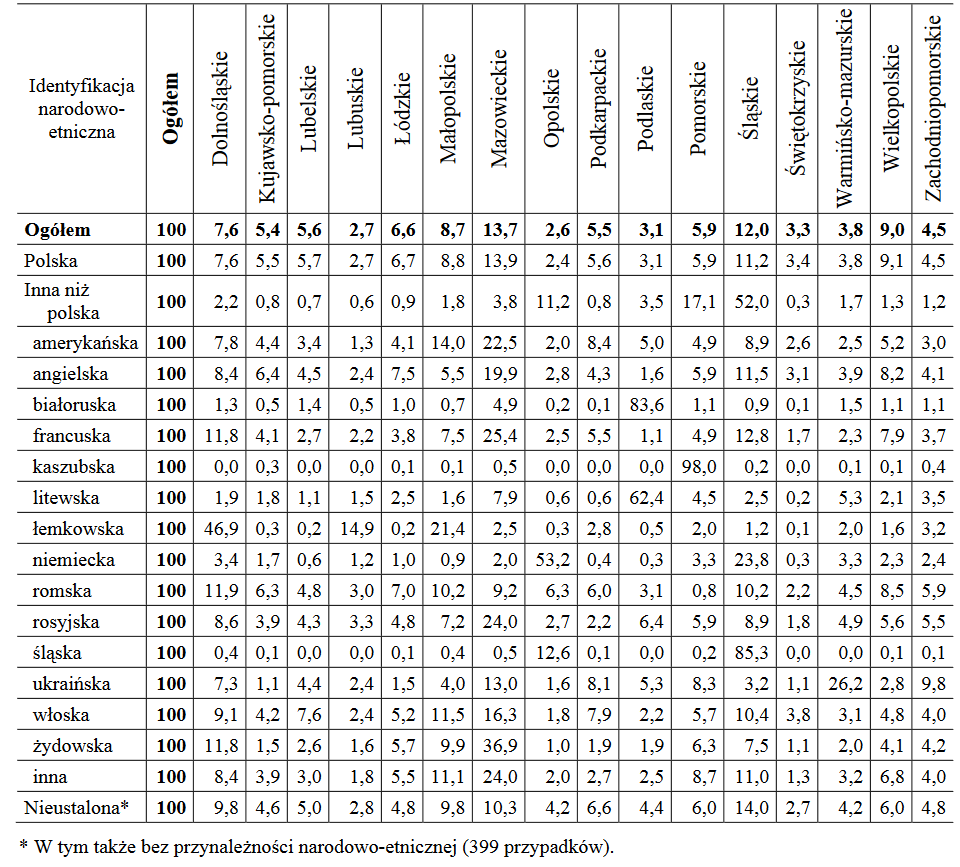
Spójrzmy jeszcze na tabelę GUS ze spisu powszechnego (za rok 2011), która informuje nas o strukturze ludności w Polsce według województw pod kątem mniejszości narodowych:

Widzimy np., że w województwie opolskim mieszka 2,6 proc. całej ludności Polski, ale aż 53,2 proc. tych mieszkańców, którzy identyfikują się jako Niemcy. W województwie śląskim mieszka z kolei 23,8 proc. krajowych Niemców (i 12 proc. wszystkich mieszkańców Polski). Spróbujmy obliczyć wskaźnik Florence'a w taki sposób, by zmierzyć koncentrację mniejszości niemieckiej w Polsce. Pamiętamy, że pomijamy te różnice, które są ujemne. Okazuje się, że są to właśnie różnice dla Opolszczyzny i Katowic, stąd nie znajdziemy w poniższym przeliczeniu różnic (2,6 - 53,2) oraz (12,0 - 23,8).

F*200 = (7,6 - 3,4) + (5,4 - 1,7) + (5,6 - 0,6) + (2,7 - 1,2) + (6,6 - 1,0) + (8,7 - 0,9) + (13,7 - 2,0) + (5,5 - 0,4) + (3,1 - 0,3) + (5,9 - 3,3) + (3,3 - 0,3) + (3,8 - 3,3) + (9,0 - 2,3) + (4,5 - 2,4) = 4,2 + 3,7 + 5,0 + 1,5 + 5,6 + 7,8 + 11,7 + 5,1 + 2,8 + 2,6 + 3,0 + 0,5 + 6,7 + 2,1 = 62,3.

Stąd F = 62,3 / 200 = 0,3115 pkt. Tak więc tu już ewidentnie jesteśmy w obszarze średnim. Co więcej, niektórzy autorzy uważają, że we wzorze na F należy dzielić nie przez 200, ale po prostu przez 100. Przy takim podejściu mielibyśmy F = 0,623 pkt, a to już oznacza wysoką koncentrację ludności niemieckiej i bardziej odpowiada naszej intuicji (ostatecznie przecież różnica między Opolszczyzną i Śląskiem a pozostałymi województwami jest w tym aspekcie uderzająca).

Z kolei wskaźnik rozproszenia / koncentracji przetwórni rybnych wyniósłby (przy dzieleniu przez 100) ok. 0,48 pkt - i to również bardziej zgadzałoby się z naszymi podejrzeniami. Oczywiście istotne jest przede wszystkim badanie zmian tego wskaźnika w czasie, a wówczas sama jego wartość, choć oczywiście ważna, nie jest kwestią kluczową (o ile tylko w każdym roku korzystamy z tej samej formuły).

A. Błaczkowska przebadała przy pomocy wskaźnika Florence'a (w wersji z dzieleniem przez 100) ofertę edukacyjną województwa dolnośląskiego w latach 2006 - 2013. Badano pięć typów szkół: zasadnicze zawodowe (w 2006 wskaźnik F dla nich wyniósł 0,102 pkt, w 2013 było 0,166 pkt), licea ogólnokształcące (odp. 0,140 pkt i 0,181 pkt), licea profilowane (odp. 0,133 pkt i 0,499 pkt), technika (odp. 0,254 pkt i 0,160 pkt) i szkoły policealne (odp. 0,525 pkt i 0,504 pkt). Przytoczmy dłuższy cytat z tej pracy:

Wyznaczony  współczynnik  rozmieszczenia Florence’a dla wszystkich szkół w 2006 roku wynosi F = 0,093, zatem wskazuje na bardzo wysoki stopień rozmieszczenia, co oznacza, że szkoły ponadgimnazjalne były w tym roku słabo skon-centrowane, a zatem ich dostępność była duża. Najsłabszą dostępnością  w tym roku  charakteryzowały się szkoły policealne (niski stopień rozmieszczenia). Najlepszym rozmieszczeniem charakteryzowały się w 2006 roku zasadnicze szkoły zawodowe, co pozwala wnioskować, że ich dostępność była dobra, a potencjalni uczniowie nie byli zmuszeni do odległych dojazdów do wybranego typu szkoły. W roku 2013 nastąpiło pogorszenie rozmieszczenia we wszystkich typach szkół, szczególnie widoczne dla liceów profilowanych. Współczynnik Florence’a dla ogółu szkół wyniósł 0,15, wskazując na wysoki stopień rozmieszczenia, ale jednak gorszy niż w roku 2006.

Przy okazji po raz kolejny widzimy, że omawiane narzędzie rzeczywiście jest przydatne i daje pewne pojęcie o tym, jak zmienia się struktura zjawisk w czasie. Oczywiście wskaźnik sam w sobie nie sygnalizuje nam przyczyn zmian, tym niemniej zwraca uwagę na sytuację i na panujące tendencje.

Adam Witczak

BIBLIOGRAFIA:

"Badania rynku", red. Z. Kędzior, Polskie Wydawnictwo Ekonomiczne 2005.

A. Błaczkowska, "Analiza przestrzennego zróżnicowania oferty edukacyjnej w powiatach województwa dolnośląskiego na tle sytuacji demograficznej – wybrane elementy", Zeszyty Naukowe Wyższej Szkoły Bankowej we Wrocławiu, Vol. 15, No. 5

D. Olewnicki, L. Jabłońska, P. Orliński, Ł. Gontar, "Zmiany w krajowej produkcji zielarskiej i wybranych rodzajach przetwórstwa roślin zielarskich w kontekście globalnego wzrostu popytu na te produkty", Zeszyty Naukowe SGGW, Problemy Rolnictwa Światowego, tom 15 (XXX), zeszyt 1, 2015.

D. Olewnicki, L. Jabłońska, P. Orliński, Ł. Gontar, "Zmiany na rynku przedsiębiorstw zajmujących się handlem hurtowym roślinami i kwiatami w Polsce", Journal of Agrobusiness and Rural Development, 1(35) 2015.

M. Wójtowicz, "Zmiany struktury przestrzennej przemysłu samochodowego Brazylii na przełomie XX i XXI wieku", Prace Komisji Geografii Przemysłu Polskiego Towarzystwa Geograficznego. 27. 38-56. (2014).

Opracowania GUS: Regiony Polski 2018, Struktura narodowo-etniczna, językowa i wyznaniowa ludności Polski 2011, Powierzchnia i ludność w przekroju terytorialnym w 2010 r.

Opracowanie "Przemysł rybny w Polsce": https://www.polagra-food.pl/pl/news/przemysl_rybny_w_polsce/?print