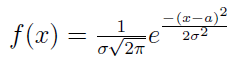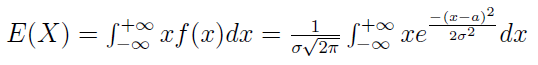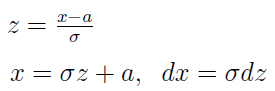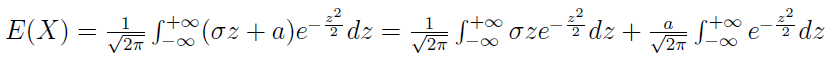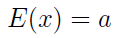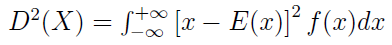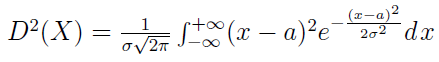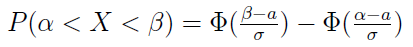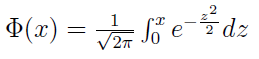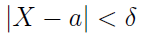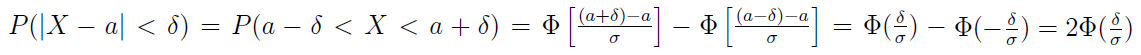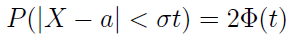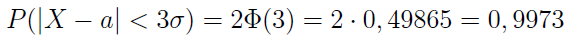Reguła trzech sigm

Rozkład normalny, zwany też rozkładem Gaussa (lub Gaussa-Laplace'a), jest jednym z najważniejszych i najbardziej znanych rozkładów prawdopodobieństwa. Często spotyka się go w naturze, przynajmniej w przybliżonej formie.

Gęstość rozkładu normalnego zadana jest następującym wzorem:

Funkcję gęstości można - w ogólności - zdefiniować np. jako pochodną z dystrybuanty, przy czym dystrybuanta w punkcie x to prawdopodobieństwo tego, że wartość zmiennej losowej nie przekroczy poziomu x.

Choć rozkład normalny jest tak powszechnie wykorzystywany, to jednak wzór na jego gęstość nie jest trywialny. W szczególności zależy on od parametrów a i σ. Jakie jest ich znaczenie?

Na bazie ogólnego wzoru możemy spróbować wyliczyć wartość oczekiwaną zmiennej losowej o rozkładzie normalnym.

Jest to całka (liczona na całej prostej rzeczywistej) z iloczynu xf(x), gdzie f(x) to właśnie gęstość zmiennej.

Wprowadźmy nową zmienną z i określmy w jej terminach odpowiednie zmienne:

Teraz możemy napisać jak poniżej:

Okazuje się, że pierwszy składnik ostatniej sumy jest zerowy - ponieważ funkcja pod całką jest parzysta, a przedział całkowania symetryczny względem początku układu współrzędnych (obrazowo mówiąc, pola pod wykresami po obu stronach znoszą się wzajemnie). Drugi ze składników jest równy a - czego nie będziemy tu szczegółowo uzasadniać; wynika to jednak z tego, że odpowiednia całka jest tzw. całką Poissona, równą pierwiastkowi z 2π.

Ostatecznie więc:

A zatem nasze a to po prostu wartość oczekiwana zmiennej. Przytoczmy jeszcze ogólny wzór na wariancję zmiennej losowej:

W naszym przypadku prezentuje się on następująco:

Dalsze obliczenia pominiemy - da się jednak pokazać, stosując m.in. całkowanie przez części i twierdzenia dotyczące szeregów, że wariancja równa jest kwadratowi liczby σ. Innymi słowy, σ to odchylenie standardowe zmiennej (pierwiastek z wariancji).

*

Da się pokazać także coś innego i nawet bardziej użytecznego. Rzecz dotyczy prawdopodobieństwa tego, że zmienna losowa o rozkładzie normalnym przyjmie wartość większą niż α i mniejszą niż β. Zachodzi następujący wzór:

Przy czym:

Funkcja Φ zwana jest funkcją Laplace'a. Jej wartości są ujęte w tablicach. Wyobraźmy sobie np., że zmienna X ma rozkład normalny, w którym wartość oczekiwana a = 30, zaś odchylenie standardowe σ = 10. Jakie jest prawdopodobieństwo tego, że zmienna X przyjmie wartość z przedziału (10, 50)? Po podstawieniu liczb i skorzystaniu z tablic okazuje się, że to 0,9544, tj. 95,44 proc. Pomocny jest tu fakt, że Φ jest funkcją nieparzystą, tj. Φ(-x) = -Φ(x). Stąd P(10 < X < 50) = 2 Φ((50-30)/10) = 2Φ(2). A to jest właśnie 0,9544.

*

Zajmijmy się teraz kolejnym zagadnieniem. Mowa o obliczeniu prawdopodobieństwa tego, że wartość bezwzględna odchylenia zmiennej (normalnej) od wartości oczekiwanej a nie przekroczy pewnej dodatniej liczby δ. Chodzi zatem o prawdopodobieństwo następującej sytuacji:

Wykonujemy następujące przeliczenia:

Wynika z tego m.in. następujący fakt: jeśli dwie zmienne losowe mają rozkład normalny z wartością oczekiwaną a = 0, to prawdopodobieństwo przyjęcia wartości z zakresu (-δ, +δ) jest większe dla tej zmiennej, która cechuje się mniejszym odchyleniem standardowym.

Przykład: załóżmy, że X ma rozkład normalny, przy czym a = 20, σ = 10. Interesuje nas prawdopodobieństwo tego, że wartość bezwzględna odchylenia X - a będzie mniejsza niż 3. Po podstawieniu danych i zerknięciu do tablic otrzymujemy: P(|X-20| < 3) = 2Φ(3/10) = 2 * 0,1179 = 0,2358.

*

Przejdźmy wreszcie do clou artykułu, tj. do reguły trzech sigm. Załóżmy, że δ, o której była mowa wyżej, to iloczyn odchylenia standardowego σ przez jakąś liczbę rzeczywistą t; w szczególności może być to wielokrotność odchylenia. To znaczy:

Mamy zatem:

Jeżeli t = 3, to otrzymujemy następujący zapis:

Naturalnie 1 - 0,9973 = 0,0027. To z kolei oznacza, że prawdopodobieństwo tego, iż odchylenie |X - a| jest mniejsze niż potrojone odchylenie standardowe zmiennej - wynosi 0,0027, czyli 0,27 proc. W praktyce jest więc bardzo niskie. Zapisuje się to w postaci tzw. reguły trzech sigm:

Jeśli zmienna losowa ma rozkład normalny, to wartość bezwzględna odchylenia tej zmiennej od wartości oczekiwanej nie jest większa niż potrojone odchylenie standardowe.

Ma to pewne znaczenie praktyczne. Otóż może być tak, że nie znamy rozkładu badanej zmiennej, ale potrafimy pokazać, że nie spełnia ona reguły trzech sigm. Wówczas nie jest ona normalna. Jeżeli natomiast spełnia tę regułę, to istnieje szansa, że jej rozkład jest normalny. Wówczas można przystąpić do stosowania innych testów, np. Shapiro-Wilka, Jarque-Bery czy Lilleforsa.

*

Wiemy skądinąd, że przy pomocy rozkładu normalnego przybliża się rozkład Bernoulliego - dla dłuższych serii. Rozkład Bernoulliego inaczej nazywamy dwumianowym (binomial). Opisuje on liczbę k sukcesów w ciągu n niezależnych prób, przy czym w każdej próbie prawdopodobieństwo sukcesu wynosi p (a więc prawdopodobieństwo porażki jest równe 1 - p). Przyjmuje się, że jeśli np oraz n(1-p) są większe niż 5, to można stosować przybliżenie rozkładem normalnym.

A zatem reguła trzech sigm stosuje się też do serii Bernoulliego. Przytoczymy dwa egzempla ekonomiczne, wzorowane na przykładach z książki M. Zakrzewskiego i T. Żaka.

W pierwszym przypadku mamy firmę ubezpieczeniową, która ubezpiecza samochody. Roczna opłata to 600 zł, odszkodowanie wynosi 12 tys. zł (oczywiście jest to bardzo prosty model). Przedsiębiorstwo ubezpiecza 850 tys. pojazdów. Prawdopodobieństwo wypadku w ciągu roku to 0,05 (dla każdego kierowcy jest takie samo) - umówmy się, że to wniosek z wieloletnich obserwacji. Zadajemy pytanie: czy firmie grozi bankructwo?

Otóż model można opisać schematem Bernoulliego: n = 850.000, p = 0,05. Wówczas np = 42.500, zaś 3σ = 3 * pierw(np(1-p)) = 3 * pierw(42.500(0,95)) =  602,8 (w przybliżeniu). Skorzystaliśmy tu ze wzoru na wariancję (i odchylenie standardowe) rozkładu Bernoulliego.

Z reguły trzech sigm wynika, że z prawdopodobieństwem 0,997 (99,7 proc.) liczba wypłat (czyli liczba "sukcesów") odchyla się od swej wartości średniej o 602,8. Ta wartość średnia to w przypadku rozkładu Bernoulliego właśnie np, tj. 42.500 dla naszych danych. Czyli na 99,7 proc. liczba wypłat będzie w zakresie (42.500 - 602,8; 42.500 + 602,8) = (41.898; 43.103) - przy czym ostatnie liczby są znów przybliżone, bez groszy. Podkreślmy dla jasności: liczba wypłat, a nie wartość każdej wypłaty (ta ostatnia jest stała, odszkodowanie to zawsze 12 tys. zł).

Gdyby więc aż 43.103 samochodów miało wypadek, to suma wypłat wyniosłaby 43.103 * 12.000 = 517.236.000 (ponad 517 milionów zł). Tymczasem wpłaty za rok to 850.000 * 600 = 510.000.000 (raptem 510 mln zł). Firma może więc mieć problem z wypłacalnością.

W oryginalnym przykładzie Zakrzewskiego i Żaka zastosowano inne liczby: roczna opłata 500 zł, odszkodowanie 10.000 zł, prawdopodobieństwo wypadku p = 0,03 oraz ubezpieczonych milion samochodów. W takim układzie suma wypłat to 305.000.000 zł, a suma wpłat to 500.000.000 zł - i wtedy nie ma zagrożenia bankructwem.

Inny przykład to bank z rezerwami wynoszącymi 100 mln zł. W ciągu miesiąca wykonuje on 10 tys. operacji, przy czym z prawdopodobieństwem 1/2 każda operacja to wpłata lub wypłata środków przez klientów, a w dodatku w grę wchodzi zawsze jednakowa kwota: 100 tys. zł. Czy realne jest ryzyko, że miesięczny bilans będzie ujemny, tj. że nie wystarczy rezerw na wypłaty?

Tym razem mamy n = 10.000 oraz p = 1/2. Liczymy 3σ = 3 * pierw(np(1-p)) = 3 * pierw(5000(1/2)) = 150. Tak więc z prawdopodobieństwem 99,7 proc. liczba wypłat (i tak samo liczba wpłat, bo p = 1/2) zawierają się w zakresie (5000 - 150; 5000 + 150) = (4850; 5150). Rozważmy więc pesymistyczny scenariusz: że to wypłat w miesiącu jest aż 5150, a wpłat tylko 4850. To znaczy, że bank wypłaca 5150 * 100.000 zł = 515 mln zł, natomiast otrzymuje w depozytach 485 mln zł. Różnica to 30 mln zł, ale bank jest w stanie ją z powodzeniem pokryć, skoro ma 100 mln zł rezerw.

Adam Witczak

BIBLIOGRAFIA:

W. J. Gmurman, "Rachunek prawdopodobieństwa i statystyka matematyczna", Wydawnictwa Naukowo-Techniczne 1975.

"Problemy rachunku prawdopodobieństwa", praca zbiorowa, PWN 1966.

B. Piłat, M. J. Wasilewski, "Tablice całek", WNT 1983

M. Zakrzewski, T. Żak, "Kombinatoryka, prawdopodobieństwo i zdrowy rozsądek", OW Quadrivium 1998