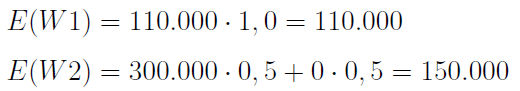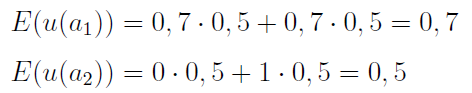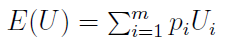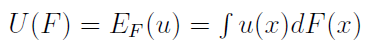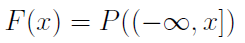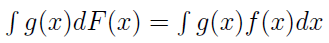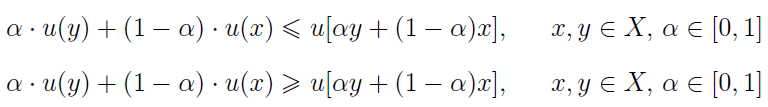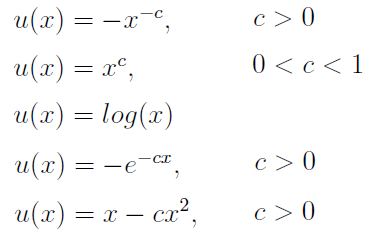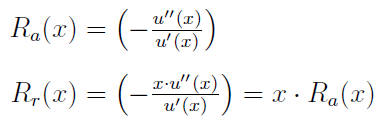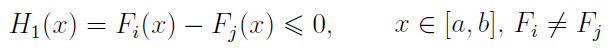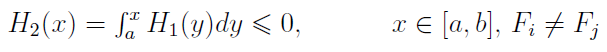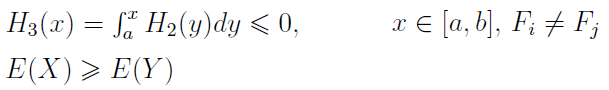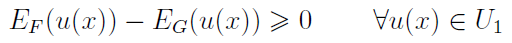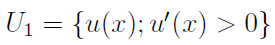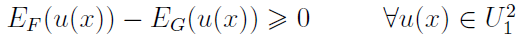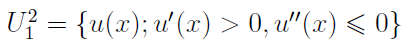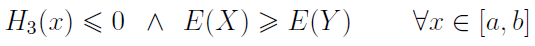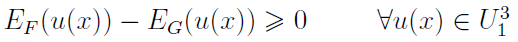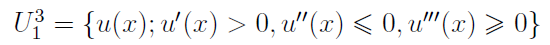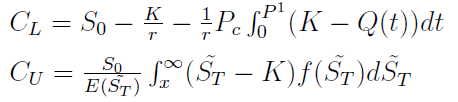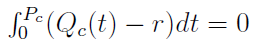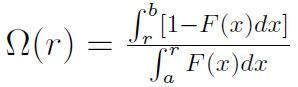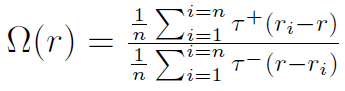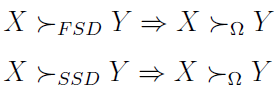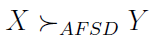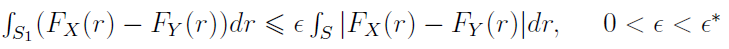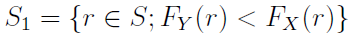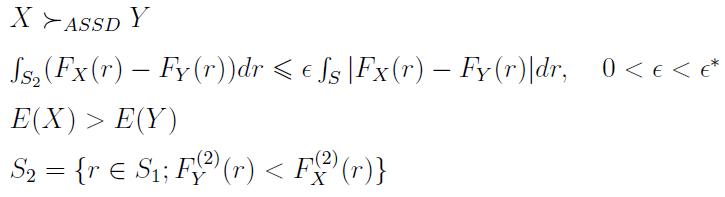Dominacje stochastyczne i użyteczność

Pojęcie dominacji stochastycznej rozważać będziemy przede wszystkim w kontekście jego wykorzystania przy badaniu użyteczności. Punktem wyjścia jest dla nas problem decyzyjny - na przykład pytanie o to, która z dostępnych inwestycji jest najlepsza.

Cóż to znaczy - najlepsza? Prosta odpowiedź w rodzaju 'taka, na której można najwięcej zarobić' okazuje się niewystarczająca i niejasna gdy tylko zagadnienie zaczyna się choć trochę komplikować.

Po pierwsze, nawet w warunkach pewności, przy braku ryzyka, maksymalizacja zysku wymaga pewnych obliczeń, niekiedy bardzo złożonych. Dobrze to widać w zagadnieniach programowania liniowego (i nieliniowego), które stosowane są np. przy zarządzaniu produkcją. Przykładem może być sytuacja, w której nasza fabryka wytwarza kilka klas produktów (np. stoły, krzesła, łóżka i szafy), różniących się kosztami, marżami czy czasem przygotowania. Zysk jest więc funkcją liczby produktów danej klasy, jednostkowego zysku na każdym produkcie, kosztów przygotowania wyrobów itd. Określenie tego, ile stołów, a ile krzeseł powinniśmy produkować, jest oczywiście możliwe, ale przecież nie banalne. Samo zagadnienie i tak jest zresztą bardzo uproszczone.

Po drugie, w warunkach niepewności czy też ryzyka zagadnienie staje się jeszcze bardziej złożone. Mowa o sytuacjach, w których mamy kilka możliwości, a każda z nich z określonym prawdopodobieństwem może przynieść pewien zysk lub pewną stratę.

Ktoś mógłby wzruszyć ramionami i powiedzieć: zróbmy tak, żeby 'średnio' wyszło na plus. Czym jest jednak 'średnia'? Powiedzmy, że chodzi o wartość oczekiwaną (a przecież takie podejście nie jest wcale jedynym czy oczywistym).

Rozważmy (przykład podajemy za pracą [Trzpiot 2011]) wybór pomiędzy dwoma scenariuszami:

W1) złożyć 100 tys. zł do banku na rok z oprocentowaniem rocznym 10 proc.

W2) ulokować te 100 tys. zł na rok w inwestycji, która z prawdopodobieństwem 50 proc. przyniesie 200 tys. zł zysku (tj. wypłata wyniesie 300 tys. zł), ale też i z takim samym prawdopodobieństwem zakończy się stratą całej sumy, tj. wypłatą równą zero.

Jeżeli będzie nas interesować wyłącznie oczekiwana wypłata (w sensie wartości oczekiwanej), to otrzymamy następujące rozwiązanie dylematu:

Jako żywo powinniśmy wybrać wariant drugi, ponieważ ma większą wartość oczekiwaną. 'Średnio' możemy zarobić 150 tys. zł.

Ale większość z nas nie poważy się na takie ryzyko. Te '150 tys. zł - przeciętnie' wydaje się nam wypłatą cokolwiek abstrakcyjną. Albo trzysta, albo... zero, nic, porażka. I ta wizja totalnej porażki dość skutecznie eliminuje skłonność do tak ostrego hazardu.

Oczywiście znajdą się i tacy, którzy faktycznie zagrają ostro. Kryteria, o których będziemy mówić, są w pewien sposób arbitralne - dane wybory są po prostu lepsze czy też najlepsze według nich; natomiast nie znaczy to, że są 'najlepsze' w jakimś absolutnym, niewzruszonym, ostatecznym sensie.

Intuicja podpowiada nam jednak, że lepiej byłoby zadowolić się spokojnym zarobkiem 10 tys. zł bez żadnego ryzyka niż szarżować. Kluczem jest tu pojęcie użyteczności wypłaty.

Funkcja użyteczności przypisuje poszczególnym możliwym wypłatom pewne liczby w taki sposób, by opisać skłonność decydenta do ryzyka. Na przykład często przyjmuje się, że funkcja użyteczności jest rosnąca i wklęsła. Drugie z tych pojęć później sformalizujemy. Na razie możemy rzecz rozumieć tak: funkcja jest rosnąca, a więc wraz ze wzrostem posiadanej sumy pieniędzy rośnie ich użyteczność. Wolimy mieć więcej niż mniej. Równocześnie jednak krańcowa użyteczność maleje. Na przykład gdy mamy 100 zł, to zyskanie kolejnych 100 zł jest sporym wydarzeniem. Ale gdy mamy 100 tys. zł, to zarobienie stu złotych jest już prawie niezauważalne. Te 'drugie' sto złotych ma dużo mniejszą użyteczność niż te pierwsze.

Wróćmy do naszego przykładu. Założmy, że użyteczność 110 tys. zł wynosi 0,7. Dla 300 tys. zł to oczywiście 1 (powiedzmy, że 1 uznajemy za maksimum), dla 0 zl to 0 (zerowa użyteczność, pusty portfel jest bezużyteczny). Można to interpretować tak: jeśli prawdopodobieństwo sukcesu naszej inwestycji będzie większe niż 0,7 - to godzimy się na scenariusz W2. Jeśli mniejsze, to pozostajemy przy W1.

Cały model możemy pojmować jako grę z naturą, która przyjmuje dwa stany: porażki i sukcesu (naszego). Tak naprawdę wpływają one (z szansą 50 proc.) tylko na scenariusz nr 2, bo w banku nie ma ryzyka, swoje 10 proc. na pewno za rok odbierzemy. A zatem:

Niejako po drodze wprowadziliśmy tu pojęcie oczekiwanej użyteczności. Widzimy, że jest ona wyższa w scenariuszu pierwszym - zgodnie z intuicją człowieka, który preferuje bezpieczeństwo ponad szaleństwo, by ująć rzecz sugestywnie.

Nie należy jednak myśleć, że taki wniosek wynika z samego faktu, że wykorzystaliśmy jakąś funkcję użyteczności. Po prostu nasza funkcja obrazuje fakt, że nie chcemy zbyt wiele ryzykować. Jak najbardziej jednak można mówić o funkcjach użyteczności także i dla takich graczy, którzy są gotowi podejmować bardzo ryzykowne czy nawet szalone kroki - i np. zawsze interesuje ich tylko scenariusz 'wszystko albo nic'. W kolejnych akapitach zajmiemy się m.in. różnymi kształtami utility function i ich interpretacją.

W ogólności przypadek dyskretny wartości oczekiwanej rozkładu użyteczności zapisujemy tak:

Przez p_i rozumiemy prawdopodobieństwo osiągnięcia i-tej wartości pieniężnej, przez U_i - użyteczność tejże wartości. Lewą stronę równania zwiemy oczekiwaną użytecznością. W przypadku ciągłym wygląda to tak:

Otóż zakłada się tu, że wypłaty opisane są zmienną losową o rozkładzie ciągłym, który ma dystrybuantę F. Przypomnijmy, że zmienna losowa to funkcja, która zdarzeniom elementarnym przypisuje elementy przestrzeni mierzalnej, w praktyce - liczby (na ogół rzeczywiste). Na przykład przy rzucie monetą mamy dwa zdarzenia elementarne: orła (możemy mu przypisać wartość 1) i reszkę (wartość 0). Prawdopodobieństwa dla obu wartości są równe 0,5.  Taki jest więc rozkład tej zmiennej: P(0) = P(1) = 0,5.

Dystrybuanta w punkcie x to prawdopodobieństwo tego, że wartość zmiennej losowej nie przekroczy poziomu t.

Czym jest w takim razie całkowanie po dystrybuancie? Otóż jeśli F ma pochodną poza być może przeliczalnie wieloma punktami, tzn. jeśli ma gęstość (ozn. f), to:

Funkcja g(x) pełni w tym ogólnym wzorze taką rolę jak u nas u(x). W dalsze rozważania z obszaru analizy matematycznej nie będziemy już wchodzić.

Dodajmy, że U(F) nazywamy funkcją oczekiwanej użyteczności Neumanna-Morgensterna, zaś u(x) to funkcja użyteczności Bernoulliego.

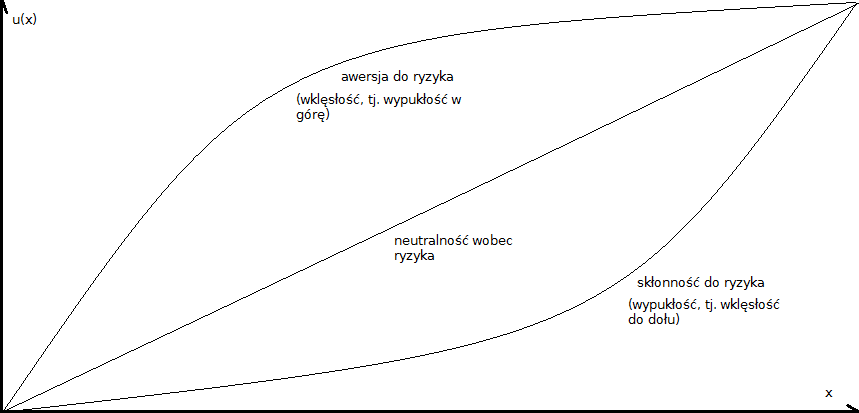
Funkcja u wypukła do góry opisuje sytuację unikania ryzyka, zaś u wklęsła do dołu - postawę szukania, podejmowania ryzyka. Uwaga: tu należy zwrócić uwagę na pewien istotny wątek terminologiczny. Otóż przez funkcję wypukłą do góry rozumiemy przypadek często zwany w literaturze funkcję wklęsłą, tj. druga pochodna jest ujemna. Funkcja wklęsła do dołu to odwrotny przypadek, często określany jako funkcja wypukła.

Widzimy to na poniższym obrazku:

Czytelnik sam może ocenić, która terminologia jest z jego punktu widzenia bardziej intuicyjna. Ostatecznie to tylko kwestia perspektywy.

Te dwa przypadki (wypukłość do góry i wklęsłość do dołu, w tej kolejności) opisuje poniższa para wzorów:

Na ogół rozważa się funkcje ciągłe i ograniczone na zbiorze X, przy czym nakłada się dodatkowe warunki, otrzymując np. klasy U₁ i U₂. Pierwsza obejmuje funkcje o pierwszej pochodnej większej od zera w obrębie wnętrza zbioru X (wnętrze to największy zbiór otwarty mieszczący się w X, przykładem może być np. przedział otwarty czy - na płaszczyźnie - koło bez brzegu). Druga to te funkcje z U₁, które mają ciągłą i ograniczoną drugą pochodną w X, a do tego owa druga pochodna jest mniejsza od zera we wnętrzu X (czyli zachodzi wypukłość w górę, tj. wklęsłość).

Konkretne przykłady funkcji z U₂ to np. funkcje: potęgowa (w dwóch wersjach), logarytmiczna, wykładnicza i kwadratowa. Widzimy je poniżej (naturalnie to również są rodziny funkcji, wzory są bowiem zależne od parametrów):

Określa się również funkcje absolutnej i relatywnej awersji do ryzyka:

O czym mówią nam te miary? Otóż jeśli bezwzględna awersja do ryzyka rośnie (maleje), to przy wzroście stopy dochodu gracze coraz mniej (więcej) środków lokuje w inwestycjach ryzykownych. Jeżeli względna awersja rośnie (maleje) to wraz ze wzrostem stopy dochodu gracz przeznacza proporcjonalnie coraz mniej (więcej) środków na przedsięwzięcia ryzykowne.

*

Przejdźmy teraz do pojęcia dominacji stochastycznych. Istnieją trzy jej stopnie. Pierwszy, obecnie zwany FSD (First Stochastic Dominance) wprowadzili w roku 1962 J. P. Quirk i R. Saposnik.

Otóż załóżmy, że zmienne losowe X i Y określone są na [a, b] i mają dystrybuanty odp. F_i, F_j. Wtedy X dominuje Y według zasady FSD (X FSD Y), gdy zachodzi warunek:

W roku 1969 zaproponowano (zrobili to J. Hadar i W. R. Russel) SSD (Second Stochastic Dominance). Tym razem warunek na X SSD Y prezentuje się następująco:

W roku 1970 G.A. Whitmoore poszedł dalej i zaproponował TSD (Third Stochastic Dominance):

Zauważmy, że pojawia się tu dodatkowy warunek na zależność pomiędzy wartościami oczekiwanymi, a poza tym obliczamy już całkę podwójną.

W odniesieniu do naszych rozważań możemy utożsamiać X i Y z rozkładami prawdopodobieństwa wypłat czy też stóp zwrotu w naszych scenariuszach inwestycyjnych. Jak to powiązać z użytecznością?

W ślad za [Trzpiot 2011] podajemy trzy następujące twierdzenia.

Twierdzenie 1.

Jeżeli zachodzi

to wówczas

gdzie

A więc zakłada się tu w odniesieniu do użyteczności jedynie tyle, że inwestor ściśe preferuje wyższe stopy zwrotu (pierwsza pochodna u jest większa od zera). Spełnienie warunki FSD gwarantuje, że inwestycja X przyniesie zyski nie mniejsze niż inwestycja Y.

Twierdzenie 2.

Jeżeli zachodzi

to wówczas

gdzie

Tu zakłada się dodatkowo, że inwestor zajmuje niechętną postawę wobec ryzyka. Funkcja jest wypukła do góry. Można ten warunek formalizować przy użyciu pojęć premii za ryzyko i wartości równoważnej, ale to pominiemy.

Twierdzenie 3.

Jeżeli zachodzi

to wówczas

gdzie

W tym twierdzeniu zakłada się, że niechęć inwestora do ryzyka maleje wraz ze wzrostem zysku. Gracz woli posiadać więcej niż mniej, ma awersję do ryzyka, ale jego bezwzględna awersja do ryzyka (przypomnijmy sobie wzór na R_a(x)) maleje. A zatem: pierwsza pochodna funkcji użyteczności u jest dodatnia (u rośnie), druga pochodna jest ujemna (u jest wklęsła, tj. wypukła w górę).

Zauważmy, że zaletą tych twierdzeń (których dowody pomijamy) jest to, iż nie wymagają one znajomości analitycznej postaci funkcji użyteczności u. Wystarczy jedynie wiedza o rozkładzie prawdopodobieństwa wypłat oraz o pewnych podstawowych cechach funkcji u, by móc wnosić coś na temat oczekiwanej użyteczności badanych inwestycji.

A co z graczami, którzy reprezentują skłonność do ryzyka, więc ich funkcje użyteczności są wypukłe (wklęsłe do dołu)? Również i dla nich znajdzie się pomoc, ale nie będziemy jej tu szczegółowo omawiać. Tą pomocą są tzw. odwrotne dominacje stochastyczne. Znów mamy trzy stopnie i trzy twierdzenia, cała konstrukcja jest podobna do tego, co widzieliśmy powyżej - aczkolwiek interesują nas tzw. odwrotne dystrybuanty.

*

Dominacje stochastyczne stosuje się również w innych zagadnieniach, np. przy wycenie opcji. Nie będziemy się w ten temat zagłębiać, ale warto przedstawić jedno z zastosowań. Chodzi o europejską opcję kupna. Przy pomocy dominacji Levy wyznaczył w roku 1985 (oczywiście pomijamy to, w jaki sposób tego dokonał, matematyki i tak jest w naszym tekście dużo) dolne i górne ograniczenie na wartość takiej opcji przy założeniu, że inwestor może równocześnie posiadać opcję lub sam instrument. W odróżnieniu od modelu Blacka-Scholesa nie mamy tu więc jednej wartości, ale przedział.

Ograniczenia dolne i górne wyglądają tak:

Oznaczenia:

S₀ - aktualna cena rynkowa instrumentu (tj. w czasie 0)

K - cena wykonania

S_T z tyldą - cena rynkowa instrumentu w momencie T (zmienna losowa)

f(S_T), S_T z tyldą - funkcja gęstości tejże zmiennej

r - stopa inwestycji wolnej od ryzyka

P¹ - to P(S_T < K), tj. prawdopodobieństwo, że cena instrumentu będzie w momencie T mniejsza od ceny wykonania

P_c to z kolei wartość wyznaczana z równania całkowego:

W tym równaniu Q_c(t) to kwantyl rozkładu stopy zwrotu opcji kupna.

Jak widać, nie są to banalne obliczenia - i oczywiście nie bardzo widać 'z zewnątrz', w jaki sposób przydały się tu dominacje. W każdym razie Levy pokazał, iż wartość uzyskiwana według Blacka i Scholesa zawsze mieści się w przedziale (C_L, C_U).

*

Warto wspomnieć o zależności pomiędzy porządkiem wyznaczanym przez dominacje stochastyczne a porządkiem generowanym przy pomocy miary Omega. O tej mierze już pisaliśmy na naszych łamach, analizując wskaźniki efektywności inwestycji. Wskaźnik Omega zaprezentowany został w pracy C. Keatinga i W. F. Shadwicka zatytułowanej A Universal Performance Measure, opublikowanej w roku 2002. Jego wzór dla przypadku ciągłego wygląda tak:

Przez F(x) oznaczamy dystrybuantę stóp zwrotu z portfela (w szczególności może to być nawet jedna akcja). Z kolei r (czasami używa się oznaczenia L) to wartość progowa stopy zwrotu - zazwyczaj po prostu stopa wolna od ryzyka. Całkowanie w teorii powinno odbywać się od -∞ do r oraz od r do +∞. Wystarczy nam jednak (a, b) jako przedział dopuszczalnych stóp zwrotu.

Zasadnicza interpretacja nie jest zawiła: im wyższa wartość Omegi, tym lepiej. To znaczy - tym bardziej efektywny jest badany portfel. Omega pełni mniej więcej taką rolę jak prostsze narzędzia w rodzaju wskaźników Sharpe'a czy Treynora.

Na podstawie danych empirycznych Omegę estymuje się następująco:

Gdy r_i - r > 0, to τ⁺ = 1, τ^- = 0 - a gdy r_i- r mniejsze lub równe od zera, to przyjmujemy odwrotne oznaczenia. Literką r_i oznaczamy stopę zwrotu z i-tej akcji w portfelu. Ogólnie można powiedzieć, że Omega to iloraz wartości oczekiwanej zysków przez wartość oczekiwaną strat - względem porównawczej wielkości r.

Można oczywiście porównywać Omegi rozmaitych zmiennych losowych, by dowiedzieć się, która z nich jest lepsza (według tego kryterium). Związek pomiędzy FSD, SSD i porządkiem wyznaczanym przez Omegę ukazują poniższe twierdzenia (wzory) z pracy [Michalska, Dudzińska-Baryła 2015]:

Jak widać, jeśli zmienna X dominuje zmienną Y w sensie FSD lub SSD, to ten sam porządek zachowany jest, gdy posłużymy się miarą Omega.

*

Oprócz dominacji (zwykłych i odwrotnych) mamy również tzw. prawie dominacje (ASD, Almost Stochastic Dominance), wprowadzone przez Leshno i Levy'ego w 2002.

Otóż prawie dominację stopnia pierwszego (AFSD) zapisujemy tak:

Zachodzi ona wtedy i tylko wtedy, gdy istnieje taki ε, że

Przez S rozumiemy łączny zbiór wyników zmiennych X i Y, zaś S1 wygląda tak:

Dla ASSD (prawie dominacji stopnia drugiego) analogiczny pakiet warunków i wzorów prezentuje się następująco:

Przez ε* rozumie się zazwyczaj parametr nie większy niż 0,5. Prawie dominacje w założeniu prezentują preferencje bardziej zgodne z intuicją niż zwykłe dominacje. Mamy tu pewne złagodzenie warunków, co bynajmniej nie upraszcza wzorów.

Adam Witczak

BIBLIOGRAFIA:

G. Trzpiot, Statystyczna analiza decyzji, Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2011

G. Trzpiot, Dominacje w modelowaniu i analizie ryzyka na rynku finansowym, Wydawnictwo Akademii Ekonomicznej w Katowicach 2006

K. Piasecki, Modele matematyki finansowej, instrumenty podstawowe, PWN 2007

K. Jajuga, K. Kuziak, P. Markowski, Inwestycje finansowe, Wyd. Akademii Ekonomicznej im. O. Langego we Wrocławiu 2008.

E. Michalska, R. Dudzińska-Baryła, Zastosowanie prawie dominacji stochastycznych w preselekcji akcji, Uniwersytet Ekonomiczny w Katowicach

M. Frasyniuk-Pietrzyk, Dominacja stochastyczna w ocenie efektywności OFE, Zeszyty Naukowe Wyższej Szkoły Bankowej we Wrocławiu, nr 20/2011

J. Dys, Dominacja stochastyczna a użyteczność, European University Institute.

E. Michalska, R. Dudzińska-Baryła, Związek funkcji Omega z dominacją stochastyczną, Studia Ekonomiczne. Zeszyty Naukowe Uniwersytetu Ekonomicznego w Katowicach, nr 237 / 2015.